без игнора умоляю
1) запишите с пи в радианах углы равнобедренного прямоугольного треугольника;
2) запишите с пи в радианах углы равностороннего треугольника;
3) запишите с пи в радианах углы прямоугольника
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание: провести наблюдение за животными записать результатам...
1 - Write the sentence. Use the Present Perfect negative with yet (uzraksti...
2 - Толық жұмыс 360 кДж, ал пайдалы жұмыс 285 кДж тең. ПӘК-ті есепте?...
3 - Для выделения всей строки необходимо щелкнуть мышью на … 1)поле...
2 - Построй треугольник со сторонами 56 мм, 68 мм и 80 мм, измерь одну...
2 - Работа по перемещению тела равна 50кДж, а пройденное расстояние...
2 - Ана система двух линейных уравнений: {y+9x=22y−9x=4 Найди значение...
2 - ЦЕЕЕ-- --|ніг----FТи-2====21-са — а---------|і———+5=пая-н=======ІНЕЕННАНЕЕНEEE-е=НЕЕ.ШЕ=-НЕЕ---НВ--Е8х...
1 - это контрольная работа❤️❤️...
2 - Волк,запряжённый в сани.составить план...
2
1) π / 4, π / 4, π / 2;
2) π / 3, π / 3, π / 3;
3) π / 2, π / 2, π / 2, π / 2.
Для решения задачи нужно знать, что1) Углы равнобедренного прямоугольного треугольника равны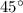 ,
, 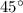 и
и 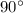 (один угол -
(один угол - 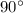 - задан в задаче, а остальные два находятся по теореме о сумме углов треугольника:
- задан в задаче, а остальные два находятся по теореме о сумме углов треугольника: 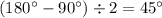 ).
).
2). Так как сумма углов треугольника равна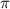 (
(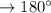 ), то если все углы равны, каждый из них равен
), то если все углы равны, каждый из них равен 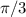 (это следует из того, что у треугольника три угла).
(это следует из того, что у треугольника три угла).
3). Все углы прямоугольника (таковых имеется четыре) равны. А сумма углов прямоугольника, как и любого четырехугольника, равна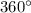 или
или 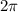 радиан. Значит, каждый угол равен
радиан. Значит, каждый угол равен 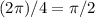 радиан.
радиан.
Или можно сразу сказать, что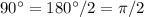 .
.