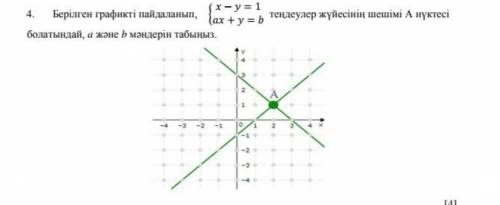
берілген графикті пайдаланып,x-y=1 ax+y=b,теңдеулер жүйесінің шешімі A нүктесі болатындай a және b мәндерің табыңыз.
Другие вопросы по теме Алгебра
Популярные вопросы
- До площини α проведено похилу АС і перпендикуляр АВ. Знайти довжину...
1 - 3. Для какого типа текста характерны слова: во-первых, я считаю,...
2 - Почему очень часто болеют на туберкулёз ВИЛ-заболевшие люди?срочьно...
1 - сделать 5 задание по буквой б( )...
3 - A lot of shops are concerned about losing goods because of s _ _...
2 - Установіть хронологічну послідовність: 1. Входження Західної України...
1 - Молю дайте ответ на 2 задание про историю качевников Мол даб история...
1 - хелп все на фото, но сделать надо УРАВНЕНИЕМ номер 7 (а)...
3 - с уравнением 25х- 100х^3=0...
3 - Ребят дали 10 минут на выполнение Западная Сибирь – один из самых...
1
Для начала, нужно заметить, что у нас дан график двух прямых.
Первое уравнение: x - y = 1
Второе уравнение: ax + y = b
Мы ищем точку пересечения этих прямых, которая обозначена на графике как A.
Для того чтобы найти значение переменных a и b, мы должны найти координаты точки A.
Шаг 1: Найдем координаты точки A.
Посмотрим на график и определим точку A. Отметим координаты точки A на графике. В данном случае, A находится по координатам (-2, -3).
Шаг 2: Подставим координаты точки A в уравнения и решим систему уравнений.
Подставляем координаты точки A в первое уравнение:
-2 - (-3) = 1
-2 + 3 = 1
1 = 1
Видим, что первое уравнение выполняется.
Теперь подставляем координаты точки A во второе уравнение:
а * (-2) + (-3) = b
Для определения значений a и b, нам не хватает информации о координате b. Однако, мы можем заметить, что линия, проведенная через точку A параллельна прямой с уравнением x - y = 1.
Мы знаем, что параллельные прямые имеют одинаковые коэффициенты при x и y. Таким образом, у нас будет следующая система уравнений:
a = 1
-2a + (-3) = b
Теперь мы можем найти значения a и b.
Подставляем a = 1 во второе уравнение:
-2 * 1 - 3 = b
-2 - 3 = b
-5 = b
Итак, найденные значения переменных:
a = 1
b = -5
Таким образом, решение системы уравнений, при котором точка A на графике имеет координаты (-2, -3), является a = 1 и b = -5.