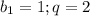B2+b6=34 b3+b7=68 sn=63 найти b1=? q=?
Другие вопросы по теме Алгебра
Популярные вопросы
- Для консервания фруктов 5 кг слив разложили в семи банках поровну .сколько...
1 - Переведите с на . простой перевод. die titelseite ist die erste seite...
3 - Выполните действие 3/4: 5/6+2 1/2*2/5-1 : 1 1/6...
2 - Легко,но 30 ! 1)найдите с перебора все делители числа 6, числа 10 и...
1 - Сколько 1/8 долей содержится в смешанном числе 9.1/8?...
2 - Ине надо просто в и-нете ответы искать! 1)диаметр окружности описанной...
2 - Составь выражение и найди их значения к сумме чисел 48 и 2 прибавь...
1 - Валентность серы в соединениях cas; so3; so2. а) 1; 2; 3. б) 2; 4;...
2 - Сочинение по личным наблюдением : в дельфинарии. план: 1.первая экскурсия...
3 - Вчем особенность этих сущиствительных задира хитрюга тихоня вредина...
3
Заметим, что b3+b7=(b2+b6)*q, тогда q=(b3+b7)/(b2+b6)=2
Теперь перепишем первое уравнение через b1, q:
b1*q+b1*q^5=34
2b1+32b1=34
b1=1
Итак, b1=1, q=2.
И, похоже, нужно еще и найти n.
Sn=b1*(q^n-1)/(q-1)=2^n-1=63
2^n=64
n=6
q=2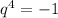
корней нет
ответ: