1. Алгебра
  2. Автомобилист выехал из а города

Автомобилист выехал из а города в город в и проехал 1/4 пути, когда вдогонку за ним отправился мотоциклист. догнав автомобиль, мотоциклист тут же повернул обратно и вернулся в город а в тот момент, когда автомобилист достиг города в . найти отношение скорости автомобиля к скорости мотоцикла, считая, что в течение всего времени движения скорости обоих транспортных средств не изменялись.

carollaim carollaim    1   22.05.2019 12:20    1

Ответы
victoria6178 victoria6178  17.06.2020 22:45

Пусть 1/4 пути равна s км , тогда весь путь равен 4s км. Пусть скорость автомобилиста равна x км\час, а скорость мотоциклиста равна y км\час (y>x). Тогда 

разность скоростей равна y-x

мотоциклист догонит автомобилиста за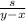 \frac{s}{y-x} час. 

После встречи автомобилисту осталось проехать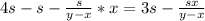 4s-s-\frac{s}{y-x}*x=3s-\frac{sx}{y-x} км

он одолеет его за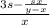 \frac{3s-\frac{sx}{y-x}}{x} час

мотоциклисту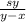 \frac{sy}{y-x} км

он одолеет его за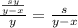 \frac{\frac{sy}{y-x}}{y}=\frac{s}{y-x}

по условию 

\frac{3s-\frac{sx}{y-x}}{x}=\frac{s}{y-x}

разделив на s получим

\frac{3}{x}-\frac{1}{y-x}=\frac{1}{y-x}

\frac{3}{x}=\frac{2}{y-x}

3y-3x=2x;3y=5x

отношения скорости автомобиля к скорости мотоциклиста

x:y=3:5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Пони0с0радушкой Пони0с0радушкой  20.12.2020 10:55
Область определения функции, заданной формулой: 1) а) y = 72-4,5x2) y = 4/4x-bb) область значений функции y = 2x+10/2На отрезке - 1 или равно X или равно 5​...
yakovlevayaninaA yakovlevayaninaA  20.12.2020 10:56
Алгебра 7 класс Заранее После приведения подобных слагвемых(8a-20b+32c) - (-18a+32b-18c) Поулчаем... (нужно выбрать ответ ниже) ▪️Другой ответ ▪️26a^2 - 52b^2 + 50c^2▪️26a-52b+50c▪️-10a+12b+14c▪️24abc​...
tetyana5 tetyana5  20.12.2020 10:58
3х^2-4х+1≥0 развяжите неравенство ХЕЛПХЕЛПХЕОПХЛЕП...
arsenagadzhanin arsenagadzhanin  31.05.2023 06:22
Освободитесь от иррациональности в знаменателе...
Камелия1231 Камелия1231  31.05.2023 06:21
Розв язати систему,яка складається з рівнянь: 2x+3y=7 i -5x+2y=11У мене 10 хв....
mansya01 mansya01  31.05.2023 06:20
ДАЙТЕ ОДИН ВАРІАНТ ВІДПОВІДІ Для функції f(x) = x³ знайдіть первісну, графік якої проходить через точку M(1; 5/4). y = 3x² + 1 y = 3x² – 1 y = x⁴/4 + 1 y = x⁴/4 – 1 y...
AmAss AmAss  31.05.2023 06:20
Спростити вираз (a+2)2+(a-6)(a+4)...
Учен586 Учен586  31.05.2023 06:20
Через яку з даних точок проходить графік рівняння 5y-3x=-1? А) (2; -1); Б) (-2; 1); В) (2; 1); Г) (-2; -1)....
камиииии76666666666 камиииии76666666666  31.05.2023 06:20
Нужна с тестом по алгебре (от )...
марьям2789 марьям2789  31.05.2023 06:20
только нормальный, понятный ответ За 7 зошитів та 4 ручки заплатили 130 грн. Після того як зошити подешевшали на 40%, а ручки подешевшали на 20%, одна ручка стала дорожчою...

Популярные вопросы