Артура вызвали к доске, учительница ушла мыть тряпку. Артур решил показать учительнице, что он самый умный в классе и знает, как делить числа и искать вероятности. Он решил написать на доске любую цифру от 1 до 8. Далее Артур рядом с этой цифрой приписывает еще одну любую цифру от 1 до Артуру найти вероятность того, что записанное двузначное число делится на 9. В ответ необходимо указать данную вероятность.
Другие вопросы по теме Алгебра
Популярные вопросы
- Система линейных уравнений 5 x = - 32 - 4 y 10 x + 4 y = - 72...
3 - Розгляньте механізм розщеплення вуглеводів у травному тракті....
2 - Допиши предложение : прессыкающиеся ящерицы,змеи,крокодилы,...
1 - Вкниге 540 страниц . андрей прочитал 135 из них . какой процент...
2 - Героїзм і мужність ознаки лицарських чеснот українських козаків...
3 - Сравните развитие стран азии в 19 веке тезисно...
1 - Примеры текстов, различающихся по размере, по оформлению, по назначению....
1 - Образуйте от глаголов существительные : петь щебетать стрекотать...
2 - Cрочно! почему деревья называют летописью природы? развернутый...
1 - Скласти твір з зарубіжної літератури на тему мої враження від...
1
1/8 ( 0,125 )
Объяснение:
Чтобы число делилось на 9 сумма его цифр должна делиться на 9.
Всего двузначных чисел мы можем составить 64 ( = 8 * 8 ).
Возможные суммы цифр среди них: 1,2,3,...16.
Из них лишь одна сумма делится на 9 - 9. Комбинаций для получения данной суммы цифр всего 8 (1;8) (8;1) (2;7) (7;2) (3;6) (6;3) (4;5) (5;4).
P = m/n; n = 64; m = 8; p = 1/8
ответ:
Объяснение:
Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть,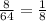 .
.