1. Алгебра
  2. Аrccos(4x²-3x-2)+arccos(3x²-8x-4)=П

Аrccos(4x²-3x-2)+arccos(3x²-8x-4)=П

sashka4erepashka sashka4erepashka    3   11.10.2020 23:24    0

Ответы
Зикош02 Зикош02  10.11.2020 23:30

\arccos(4x^2-3x-2)+\arccos(3x^2-8x-4)=\pi

\arccos(4x^2-3x-2)=\pi -\arccos(3x^2-8x-4)

Используя свойство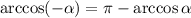 \arccos(-\alpha )=\pi-\arccos \alpha, получим:

\arccos(4x^2-3x-2)=\arccos(-3x^2+8x+4)

ОДЗ:

\begin{cases} -1\leq 4x^2-3x-2\leq1 \\ -1\leq-3x^2+8x+4\leq1 \end{cases}

Учитывая это ограничение можно перейти от равенства арккосинусов к равенству их аргументов:

4x^2-3x-2=-3x^2+8x+4

7x^2-11x-6=0

D=(-11)^2-4\cdot7\cdot(-6)=121+168=289

x_1=\dfrac{11+17}{2\cdot7} =2

x_2=\dfrac{11-17}{2\cdot7} =-\dfrac{3}{7}

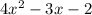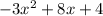При полученных значениях х выражения 4x^2-3x-2 и -3x^2+8x+4 равны. Остается проверить, принимают ли они значения из отрезка от -1 до 1.

4\cdot2^2-3\cdot2-2=16-6-2=8\notin[-1;\ 1] - посторонний корень

4\cdot\left(-\dfrac{3}{7}\right) ^2-3\cdot\left(-\dfrac{3}{7}\right) -2=4\cdot\dfrac{9}{49}+\dfrac{9}{7} -2=\dfrac{36}{49}+\dfrac{63}{49} -\dfrac{98}{49} =\dfrac{1}{49} \in[-1;\ 1]

Итак, единственный корень уравнения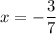 x=-\dfrac{3}{7}.

ответ: -3/7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ahun2001ahun ahun2001ahun  13.03.2019 07:55
По 7 класс.в треугольнике авс внутренние углы при вершине в равен углу с=61°, угл в=49°найдите внешний угл при вершине а.​...
chukovsema chukovsema  13.03.2019 07:58
Втеореме написано числа рвнобедренного треугольника что его 2 стороны это следовательно вторая см 3 ​...
kristinkalubaya kristinkalubaya  13.03.2019 09:00
Докажите,что при всех допустимых значениях переменной выражение (36/x^2-/x-6)+6/x принимает одно и тоже значение,найдите его....
Samisha Samisha  13.03.2019 07:58
Прощу ! найти первый наибольший по длинет непрерывный числовой промежуток, все числа из которого неотрицательны и являются решениями неравенства sin(4x-пи/3) 0...
Виолакеса Виолакеса  13.03.2019 09:00
Есть колба 14 мл, 9мл и 5мл. как получить 7 мл в колбе объёмом 14 мл?...
GanifaGasanova505 GanifaGasanova505  13.03.2019 09:00
Один килограмм сыра стоит х рублей. составьте выражение для вычисления стоимости n г этого сыра (в р.)...
svitlanakost svitlanakost  13.03.2019 09:00
Найдите cosα , если sinα = -24/25 и α принадлежит (пи; 3пи/2)...
dima102603 dima102603  13.03.2019 09:00
Периметр треугольника равен 63 см. одна сторона равга 18 см, что на 7 см меньше второй стороны. найдите третью сторону треугольника. напишите ответ полность, заранее...
2Znanijacom1 2Znanijacom1  13.03.2019 08:04
Буду вам признателен 25 на рисунке ab\\ cd. найдите градусную меру углов mka и cmk ?...
annamos16 annamos16  13.03.2019 08:05
Решить уровнение общей формулой 4× в квадрате-2×-3=0 ​...

Популярные вопросы