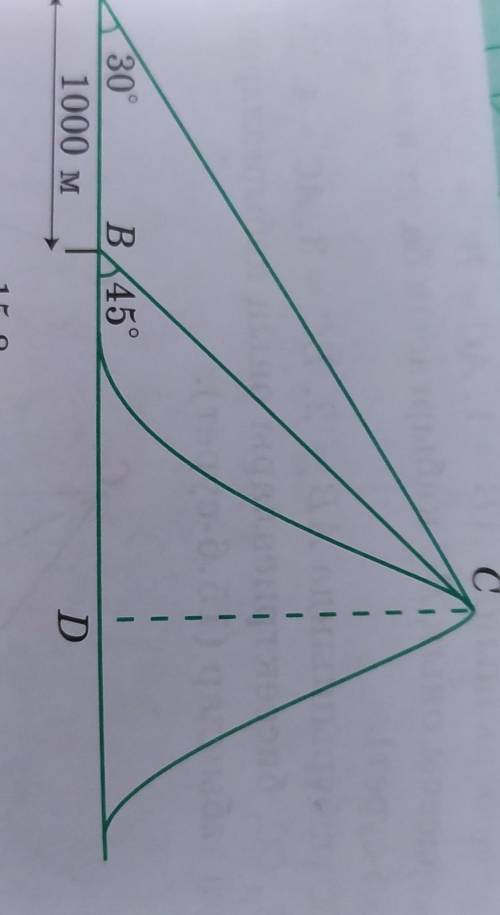
Қандай да бір нүктеден таудың төбесі 30° бұрышпен көрінеді.
Тауға 1000 м жақындағанда тау-
дың төбесі 45° бұрышпен көрінді.
Таудың биіктігін жуықтап та-
быңдар (15.18 сурет) Жауабында
метрді бүтін санмен көрсетіңдер.
Другие вопросы по теме Алгебра
Популярные вопросы
- Построить предложения по образцу. Все даты прописать словами! Johannes Kepler...
3 - 1)Выразите переменную х через переменную у из уравнения -6у +3х = 24 * а)х...
2 - Помагите пожайлуста пожайлуста көмектесіңіздер берем өтінемін...
2 - Тринадцатый Подвиг Геракла...
3 - Запишите глаголы по группам: 1) глаголы с суффиксом -ова- (-ева); 2) глаголы...
2 - Побудуйте в одній системі коордитат графіки функцій y= x-1 і y= 1 x+2 та...
1 - ТЕСТ ПО ЛИТЕРАТУРЕ Саша Черный «Кавказский пленник» Укажите настоящую фамилию...
1 - Упр 1,2стр112читать ,переводить,новые слова записывать в словарь,упр.3стр.113письменно.Упр1,стр.114...
1 - ответить на во по географии...
3 - Под каким углом косинуса и синуса нужно правильно дрошит? ответ в градусах...
3
Давайте разберем эту задачу пошагово.
У нас есть три треугольника на картинке: ABP, CDP и CEP.
Первый треугольник ABP - прямоугольный треугольник, так как угол P равен 90°. Мы знаем, что угол B равен 30°.
Для решения задачи нам нужно найти высоту треугольника ABP (h1), чтобы затем найти высоту треугольника CDP (h2) и высоту треугольника CEP (h3), и наконец, сравнить их.
1) Найдем высоту треугольника ABP (h1):
Для этого мы можем использовать тригонометрическое соотношение тангенса:
тангенс угла B = h1 / AB
тангенс 30° = h1 / AB
√3 / 1 = h1 / AB
√3AB = h1
2) Теперь найдем высоту треугольника CDP (h2):
Мы знаем, что треугольник CDP является подобным треугольнику ABP. Поэтому отношение сторон в этих треугольниках будет одинаковым:
h2 / CD = h1 / AB
h2 / 1000 = √3AB / AB
h2 / 1000 = √3
h2 = 1000 * √3
h2 ≈ 1732 метра
3) Наконец, найдем высоту треугольника CEP (h3):
Аналогично, треугольник CEP подобен треугольнику CDP и отношение сторон будет равно:
h3 / CE = h2 / CD
h3 / 1000 = h2 / CD
h3 / 1000 = 1732 / 1000
h3 ≈ 1732 метра
Таким образом, биение тауды (высота) равно 1732 метра.