Алгебра, 8 класс
При каких значениях х верно неравенство
Решите подробно
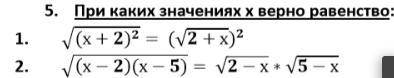
Другие вопросы по теме Алгебра
Популярные вопросы
- Вот это сор по английскому языку ...
3 - В. Драгунский Девочка на шаре ...
1 - Самостоятельно проведите доказательство и исследование. паже 7 класс. ...
3 - Сделайте 6 класс Английский язык смотрите фото 35 отдал поинтов ...
2 - В таблице представлены результаты учащихся за экзамен по математике число...
3 - ПИШИТЕ только ТЕ, КТО реально ЗНАЕТ ОТВЕТ!)...
2 - Один из учащихся 8-го класса за две четверти получил такие оценки по математике:...
3 - Определите возраст дерева, спил которого размещен ниже: ...
3 - Зробіть синтаксичний розбір речення:Люди, напевно, завжди любитимуть барвисту...
2 - В схеме значения ЭДС E1=2 B, E2=3B, а их внутренние сопротивления равны...
1
одз вспомним
1. 2 + x >= 0
x >= -2
√(x + 2)² = (√(2 + x))²
|x + 2| = x + 2
при x >= -2 |x + 2| = x + 2
x + 2 = x + 2
x ∈ [-2, +∞)
2. √((x - 2)(x - 5)) = √(2 - x) * √(5 - x)
одз (x - 2)(x - 5) ≥ 0
[2] [5]
x ∈ (-∞, 2] U [5, +∞)
2 - x >=0
x <= 2
5 - x >=0
x <= 5
x ∈ (-∞, 2]
√(x - 2)(x - 5) = √(2 - x)* √(5 - x)
√(x - 2)(x - 5)² = √(2 - x)²* √(5 - x)²
(x - 2)(x - 5) - (2 - x)* (5 - x) = 0
x <= 2
x = 5 нет
ответ х <= 2