Алгебра 11 класс . объясните Ваши действия и шаги ( ну там, какие именно правила использовали) я хочу понять, как решить самому похожие задания!
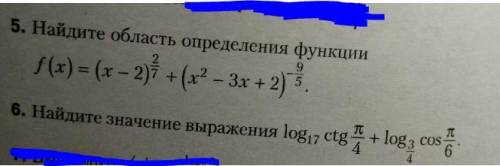
Другие вопросы по теме Алгебра
Популярные вопросы
- Где находятся центры регуляции обмена веществ...
1 - Скакой скоростью движутся электроны в кинескопе телевизора при ускоряющем...
2 - Сочинить сочинение на тему день моей мамы....
2 - Укости 304 марки в двух альбомах помещается по 47 марок с рыбами...
1 - Жёлтый цвет семян и их гладкая форма доминируют. определите генотип...
3 - Составить диалог по языку ,,в кафе...
1 - Кто повесил свой щит на цари кратких воротах...
1 - Краствору содержащему карбонаь натрия массой 10,6 г прилили раствор...
2 - Решить)! только все 1. решите уравнение 4(3-x)-11=7(2x-5) 2. решите...
3 - Что является объектом восприятия,а что -фоном ?...
1
5) Для решения задач подобного типа, нужно знать ограничения (знаменатель не нуль, аргумент логарифма > 0 и т.д.). В данном случаев, если выражение возводится в рациональную степень, то оно >=0
Помним, что:
Пересекаем
6) Вспомним, что:
Перепишем выражение:
5) Для решения задач подобного типа, нужно знать ограничения (знаменатель не нуль, аргумент логарифма > 0 и т.д.). В данном случаев, если выражение возводится в рациональную степень, то оно >=0
Помним, что:
Пересекаем
6) Вспомним, что:
Перепишем выражение: