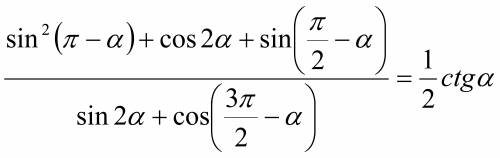
Алгебра: Алгебра 10 класс, доказать тождество

Алгебра 10 класс, доказать тождество

Ответы

KV4 20.06.2021 01:13

Объяснение:

$\frac{\sin ^{2} (\pi {- }\alpha ) + \cos 2\alpha + \sin( \frac{\pi}{2}{ - }\alpha ) }{ \sin2 \alpha + \cos(\frac{3\pi}{2} - \alpha ) } = \frac{1}{2} \ctg \alpha \\$

Преобразуем левую часть:

$\frac{\sin ^{2} (\pi {- }\alpha ) + \cos 2\alpha + \sin( \frac{\pi}{2}{ - }\alpha ) }{ \sin2 \alpha + \cos(\frac{3\pi}{2} - \alpha ) } = \\ = \frac{\sin ^{2} \alpha + ( \cos^{2} \alpha - \sin^{2} \alpha ) + \cos\alpha }{ 2\sin \alpha \cos \alpha - \sin \alpha } = \\ = \frac{\cancel{\sin ^{2} \alpha \: } + ( \cos^{2} \alpha - \cancel{\sin^{2} \alpha }) + \cos\alpha }{ \sin \alpha (\cos \alpha - 1) } = \\ = \frac{ \cos^{2} \alpha + \cos\alpha }{ \sin \alpha (2\cos \alpha - 1) } = \frac{ \cos \alpha (\cos\alpha+1) }{ \sin \alpha (2\cos \alpha - 1) }= \\=\frac{\cos\alpha+1 }{ 2\cos \alpha - 1 } \cdot\frac{ \cos \alpha}{ \sin \alpha} = \frac{\cos\alpha+1 }{ 2\cos \alpha - 1 }\cdot\ctg \alpha =\\ = \frac{(\cos\alpha-0,5)+1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \frac{(\cos\alpha-0,5) }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha+\frac{1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \frac{1 }{ 2}\cdot\ctg \alpha+\frac{1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \bigg( \frac{1 }{ 2}\cdot\ctg \alpha\bigg)+\frac{3 }{ 4\cos \alpha - 2)}\cdot\ctg \alpha$

Это максимум. Левая и правая части, очевидно, не совпадают (в скобках выделено выражение совпадающее с правой частью, но сдева также есть дополнительные члены, отсутствующие справа)

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра