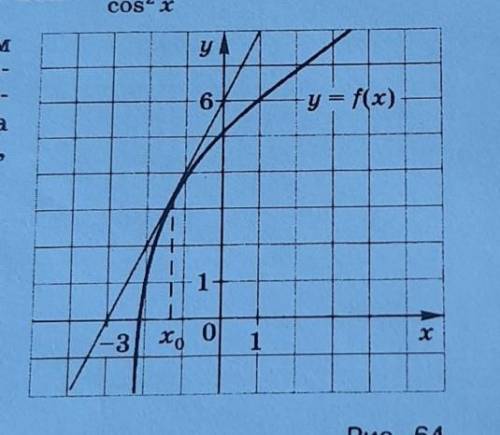
A12. Пользуясь графиком функции y=f(x), к ко-
торому в точке саб-
сциссой хо проведена
касательная (рис. 64),
найдите f'(хо).
1) f(x) = 6;
2) f'(x) =- 2;
3) f (x) =— 3;
4) f'(хо) = 2.​

Чтобы ответить на этот вопрос, нужно использовать определение производной функции в точке.

Производная функции в точке обозначается как f'(x) или dy/dx и представляет собой скорость изменения функции в данной точке.

Для нахождения значения f'(хо) нужно найти уравнение касательной линии и найти его угловой коэффициент, который будет равен f'(хо).

Просмотрим график функции y=f(x). Касательная проведена к функции в точке с абсциссой хо. Мы хотим найти f'(хо), поэтому нам необходимо найти угловой коэффициент касательной линии.

Определение говорит нам, что угловой коэффициент касательной равен производной функции в данной точке. Давайте рассмотрим каждый вариант ответа и найдем соответствующую производную.

1) f(x) = 6
Если f(x) равна константе 6, то функция является прямой линией с постоянным значением 6. Значит, производная f'(x) будет равна нулю. Следовательно, f'(хо) = 0.

2) f'(x) = -2
Условие 2 означает, что производная f'(x) равна -2 для всех значений x. Это означает, что функция имеет постоянную скорость изменения и является наклонной линией. Угловой коэффициент такой линии равен -2. Следовательно, f'(хо) = -2.

3) f(x) = -3
Если f(x) равна константе -3, то функция также является прямой линией с постоянным значением -3. Значит, производная f'(x) будет равна нулю. Следовательно, f'(хо) = 0.

4) f'(хо) = 2
Это прямое указание на значение производной f'(хо). Значит, угловой коэффициент касательной линии равен 2. Следовательно, f'(хо) = 2.

Итак, касательная, проведенная к функции в точке с абсциссой хо, имеет угловой коэффициент, равный f'(хо).

Ответы на вопрос:
1) f'(хо) = 0.
2) f'(хо) = -2.
3) f'(хо) = 0.
4) f'(хо) = 2.