а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
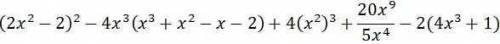
Другие вопросы по теме Алгебра
Популярные вопросы
- Какая стрелка указывает направление вектора линейной скорости тела в точке Мира...
2 - У душистого горошка высокий рост (Т) доминирует над карликовым (t), зеленая окраска...
1 - Сенкан на тему фізикаМає бути таких 5!наприклад :Веселка...
3 - )) лабораторный метод получения хлороводорода: а) хлор + водород; б) бертолетовая...
3 - Төменде берілген тақырып бойынша зерттеу жұмысын дайында. Зерттеу тақырыбы Windows...
1 - Выразите t из формулы s=gt^2/2 (свободное падение тел ....
2 - Раскрой скобки и представь в виде дроби (g+g/u)`2...
1 - Определи, на сколько градусов нагреется вода объёмом 3 л, если ей сообщить количество...
2 - А : 3-тапсырма. Парталасыңмен Қазтуған жыраудың монологіндиалогке айналдырып, сұрақ-жауап...
2 - Вычислить массу CaO полученного при термическом разложении 200г CaCo3 содержащего...
1
В решении.
Объяснение:
а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
(2х² - 2)² - 4х³(х³ + х² - х - 2) + 4(х²)³ + 20х⁹/5х⁴ - 2(4х³ + 1) =
= 4х⁴ - 8х² + 4 - 4х⁶ - 4х⁵ + 4х⁴ + 8х³ + 4х⁶ + 4х⁵ - 8х³ - 2 =
= 8х⁴ - 8х² + 2. Стандартный вид. Степень (х⁴) = 4.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
Так как коэффициенты при х чётные (8 и 8) и число 2 также чётное, при любых значениях х многочлен делится на 2.
в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
Так как 8х⁴ > 8х² и степени при х чётные, то есть, сами одночлены в составе многочлена не могут быть отрицательными, при любых действительных значениях x многочлен не может принимать отрицательных значений.