а) Найдите наибольшее значение выражения. При каких значениях переменных оно достигается?
б) Найдите наименьшее значение выражения. При каких значениях переменных оно достигается?
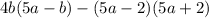

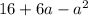

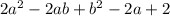
Другие вопросы по теме Алгебра
Популярные вопросы
- Які риси характеру богатирів ви могли б назвати дивлячись на скульптуру...
1 - Складіть складну юридичну ситуацію з запитанням і розв язання її...
2 - Стр 113 упр 6 класс 6 Составьте предложения с данными словосочетаниями....
1 - Длина оконного стекла 22 дм, а ширина со-ставляет половину длины. Чему...
1 - Перебудувати речення у без особове Грім струсонув землю ...
3 - Вычислите значение выражения 10x(x - 3) - 2,5x(4x - 2) при...
2 - Дано паралельну проекцію рівнобедреного трикутника. Побудувати проекцію...
2 - 46. Запишіть у дві колонки слова, які починаються: 1) на м який приголосний;...
3 - до ть написати таблицю,право 9 клас...
2 - 6) ax – bx – cx – ay + by + cy.Разложить на множители группировки многочлены...
2
а) 4 при a = 2k, b = 5k; 4 при a = b = 2; 25 при a = 3;
б) 1 при a = 3; 1 при a = b = 1
Объяснение:
а)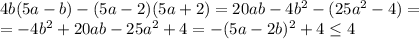
Наибольшее значение (4) достигается, когда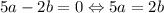 , то есть подходят все пары вида a = 2k, b = 5k. Например, максимальное значение достигается при a = 2, b = 5.
, то есть подходят все пары вида a = 2k, b = 5k. Например, максимальное значение достигается при a = 2, b = 5.
Наибольшее значение (4) достигается, когда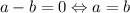 и
и  , то есть при a = b = 2.
, то есть при a = b = 2.
Наибольшее значение (25) достигается, когда .
.
б)
Наименьшее значение (1) достигается при
Наименьшее значение (1) достигается, когда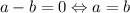 и
и  , то есть при a = b = 1.
, то есть при a = b = 1.