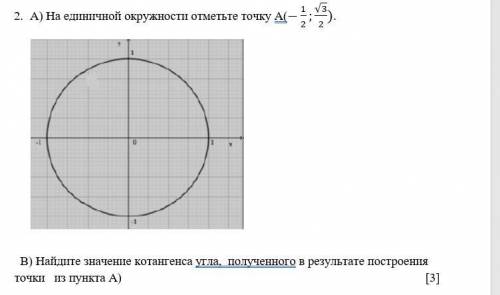
А) На единичной окружности отметьте точку А(-1/2;√3/2). В) Найдите значение котангенса угла, полученного в результате построения точки из пункта А)

Для начала, давайте разберемся с пунктом А.
У нас есть единичная окружность, то есть окружность с радиусом 1. Центр этой окружности находится в точке (0, 0).

Точка А(-1/2;√3/2) задана в декартовой системе координат. Значение x-координаты равно -1/2, а значение y-координаты равно √3/2.

Теперь давайте нарисуем оси координат и построим на них единичную окружность.
Ось X будет горизонтальной и проходит через центр окружности (0, 0).
Ось Y будет вертикальной и также проходит через центр окружности (0, 0).

Точка А будет находиться во второй четверти окружности, так как ее x-координата отрицательная, а y-координата положительная.

Теперь найдем расстояния от центра окружности до точки А.
Расстояние по горизонтали равно |x-координата|, то есть |-1/2| = 1/2.
Расстояние по вертикали равно |y-координата|, то есть |√3/2| = √3/2.

Теперь, используя найденные значения расстояний, мы можем на единичной окружности отметить точку А.
Найдем точку на окружности, которая находится на расстоянии 1/2 по горизонтали от центра окружности.
Эта точка будет иметь координаты (-1/2, 0).

Затем найдем точку на окружности, которая находится на расстоянии √3/2 по вертикали от центра окружности.
Эта точка будет иметь координаты (0, √3/2).

И, последнее, соединим эти две точки линией, чтобы получить линию, проходящую через точку А и центр окружности.

Теперь перейдем к пункту В, где нужно найти значение котангенса угла, полученного в результате построения точки А.

Котангенс - это отношение катета противоположного углу к катету прилежащему к нему.
Так как мы знаем координаты точки А и центра окружности, мы можем найти эти катеты.

Катет, противоположный углу, будет равен расстоянию по вертикали от центра окружности до точки А. Это √3/2.

Катет, прилежащий к углу, будет равен расстоянию по горизонтали от центра окружности до точки А. Это 1/2.

Теперь, используя найденные значения катетов, мы можем посчитать котангенс угла.

Котангенс = противоположный катет / прилежащий катет
Котангенс = (√3/2) / (1/2)
Котангенс = (√3/2) * (2/1)
Котангенс = √3

Таким образом, значение котангенса угла, полученного в результате построения точки А, равно √3.