(a²+b²)(c²+d²)=(ac+bd)²+(ad-bc)² докажите тоджество
и лучший ответ
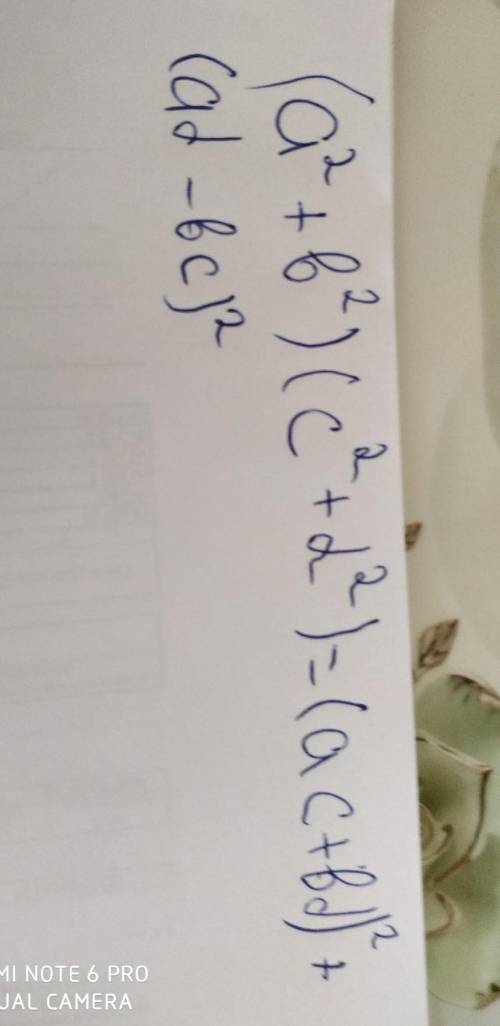
Другие вопросы по теме Алгебра
Популярные вопросы
- Ивот с этими . 6 плюс 4a-5 плюс a-7a....
2 - Постройте отрезок ав =15 см.отметьте на этом отрезке точки с, д, м так , чтобы ас...
1 - 3(4-m)(4+m) -5(x+y)(y-x) 2m(3a-5)(3a+5)...
1 - Цена одного килограмма сыра 90 руб. 40 коп. 1 килограмма колбасы в 2 раза дороже...
2 - Название карней на котором находяться корни волос и что они необходимы?...
3 - ответить на вопросы жақын арада спорт бәсекелері бола ма ? сіздерде қай ойынды көбірек...
3 - Морфологический разбор предложений: в первом классе,восьмое марта,к четырём мальчикам,к...
2 - Решите ,выполни буквенную запись наречий со словами: начист[а], нагол[а], искос[а],...
3 - Как решить бабкшка родилась в 1935 году. дедушка на5 лет старше бабушки. в каком...
2 - Выразите в метрах 480 км 480 дм 480 см 480 мм 525 км 525 см дм мм 3 км дм см мм...
3
Смотри......................
Решение и ответ:
Докажем, что правая часть равна левой:
Правая часть равна левой, что следовало доказать: