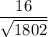А (3; -2; -1), В (-5; -2; 1), С (-1; 5; 5), D (2; -4; 1). Чему равен cos угла между прямыми АВ и CD?
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите уранение: 7 целых 1/2 : на 4 целых 1/2 = х : 8 целых 1/3....
2 - Из суммы чисел 35 и 3 вычти 20. к разности чисел 82 и 13 прибавить...
3 - Площа поля становить 720 га. перша бригада трактористів зорала 4/9...
3 - 20пнкт ! краткое сообщение об органе (муз инструменте)...
1 - Длина прямоугольника 56 см.ширина составляет 7/8 длины.найдите ширину...
2 - Спортсмен сделал 36 выстрелов из них одна шестая часть промохов...
2 - Масса фосфина ph3 равна 17г. выполните все возможные вычисления...
2 - Необхідно знайти спільнокореневі слова до слова камінь, щоб змінити...
3 - Решить : на одной автостоянке было а 4 раза меньше машин, чем на...
1 - Исправьте ошибку в ответе ученика в корне слова померить (друзей)...
3
Косинус угла между прямыми, задаваемыми направляющими векторами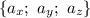 и
и 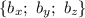 :
:
Определим направляющие векторы:
Найдем искомый косинус:
ответ: