9 класс Определите количество членов последовательности, расположенных между а3(k+2) и а3(k+6).
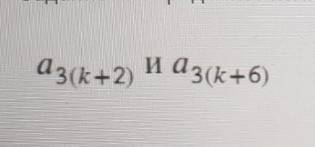
Другие вопросы по теме Алгебра
Популярные вопросы
- Чтобы перевезти кирпич на стройку нужно было 10 печатных машин на три дня причем...
2 - 1.какой известный писатель был тесно связан с нефтяной промышленнотью 2.какое...
3 - Общее наименование соматических клеток? ?...
1 - Периметр треугольника abc равен 29 см. найдите стороны треугольника, если ab+bc=19(...
1 - 7класс. примеры тел, движущихся относительно земли; неподвижно относительно...
3 - Составить 5предложений с однородными членами...
3 - Словосполучення з поданих слів: три (сценарій), півтора (день), четверо (сестра),...
3 - +8-20)= найдите значение выражение....
3 - 4+1 5 знак больше и меньше какое чисдо будет?...
2 - По широкой тополевой аллее ср. р., д. идем к монументу -величественной фигуре...
3
В данной задаче у нас дано, что a1 = 3, a2 = 4 и a3 = 7.
Чтобы найти a4, мы можем использовать формулу рекуррентности, которая определяется как a(n) = a(n-1) + a(n-2). В нашем случае:
a4 = a3 + a2 = 7 + 4 = 11.
Аналогично, мы можем найти значения a5 и a6, используя ту же формулу:
a5 = a4 + a3 = 11 + 7 = 18,
a6 = a5 + a4 = 18 + 11 = 29.
Теперь у нас есть значения всех шести членов последовательности от a1 до a6.
Чтобы найти количество членов последовательности между a3(k+2) и a3(k+6), нам нужно вычислить значение k исходя из данного уравнения:
a3(k+2) = 11,
a3(k+6) = 29.
Для этого выражения нам понадобится еще одно уравнение, чтобы избавиться от переменной k. Мы знаем, что a4 = a3 + a2, поэтому:
a3(k+3) = a3(k+2) + a2.
Используя это уравнение и уравнения a3(k+2) = 11 и a3(k+6) = 29, мы можем составить систему уравнений и решить ее:
a3(k+3) = a3(k+2) + a2 => 7(k+3) = 11 + 4 => 7k + 21 = 15 => 7k = -6 => k = -6/7.
Таким образом, мы нашли значение k. Теперь мы можем найти количество членов последовательности между a3(k+2) и a3(k+6).
Используя значение k = -6/7, мы можем вычислить значение a3(k+2) и a3(k+6):
a3(k+2) = a3(-6/7 + 2) = a3(8/7) = a3 + a2 = 7 + 4 = 11,
a3(k+6) = a3(-6/7 + 6) = a3(36/7) = a3 + a4 + a5 + a6 = 7 + 11 + 18 + 29 = 65.
Теперь нам осталось вычислить количество членов последовательности между a3(k+2) и a3(k+6), используя найденные значения:
Количество членов = a3(k+6) - a3(k+2) - 1 = 65 - 11 - 1 = 53.
Таким образом, количество членов последовательности, расположенных между a3(k+2) и a3(k+6), равно 53.