1. Алгебра
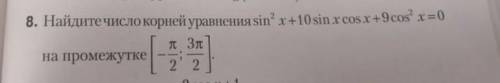
  2. 8 задание.Тригонометрия.

8 задание.Тригонометрия. ​


8 задание.Тригонометрия. ​

superyg superyg    1   23.12.2020 22:37    0

Ответы
angelinamikhay angelinamikhay  22.01.2021 22:38

4

Объяснение:

Это однородное тригонометрическое уравнение. Решается путем деления обеих его частей на cos² x, не равный 0.

\sin {}^{2} (x) + 10 \sin(x) \cos(x) + 9 \cos {}^{2} (x) = 0

После деления получим

\tan {}^{2} (x) + 10 \tan(x) + 9 = 0

Откуда

\tan(x) = - 1

\tan(x) = - 9

В первом уравнении

x = \frac{3\pi}{4} + \pi \: n

Во втором

x = - arctan(9) + \pi \: k

Эти корни принадлежат либо 2-й, либо 4-й четверти. То есть, во второй четверти будет два корня из каждой серии, и в 4 четверти будет два корня из каждой серии.

Значит, промежутку принадлежат четыре корня данного уравнения.

Как-то так!

В качестве благодарности сойдёт лайк и 5 звёзд

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kanzmak kanzmak  11.08.2019 11:20
Найти корни уравнений 12 (х – 3) + 4 (5 – х) = 2 (4 – х) ; 4 (х – 3) – 2 (5 – 3х) + 7 = 3 (3х – 5) + х ; 27 – 3 (4х – 5) + 2 (7 – х) = 7 (3 – 2х)...
tokio272 tokio272  11.08.2019 11:20
1)построте график функций у=3/8х(дробь)2)найдите по графику значение функции при х, равном: 4,6,8,-4....
juliakolesnik04 juliakolesnik04  11.08.2019 11:20
За 3 тетради и 5 карандашей саша заплатил 29 рублей, а таня за 1 тетрадь и 7 карандашей 31 рубль. сколько стоит тетрадь и сколько стоит карандаш? (решить системой)...
Анигелятор228 Анигелятор228  11.08.2019 11:20
2y-3/6y=2y-1/2-2y-1/3 решите уравнение...
Sasha808621 Sasha808621  11.08.2019 11:20
√15 * √30 * √18 + 1,5√1 целая 11/25 вычислите...
MillaGuper MillaGuper  11.08.2019 11:20
√2/5*√42/11*√77/15-3,2√1 9/16 вычислите...
skotnikova04 skotnikova04  11.08.2019 11:20
Вычислите значение 1/4х-(х+1/2y) при х=2,4 и у= -4,4...
Lolkekcheburecks Lolkekcheburecks  11.08.2019 11:20
Среди указаных скоростей выберите ту, которая вдвое меньше какой либо другой из перечисленых 1) 1км/мин ; 2) 20м/с ; 3) 300 м/мин. ; 4) 30 км/ч...
Golden12345 Golden12345  11.08.2019 11:30
Если сумма 2016 натуральных чисел равна 2017, то их произведение равно: 1, 2, 2016, 2017. заранее !...
тупой172 тупой172  11.08.2019 11:30
Снова! нужна с уравнением 3(0,9x - 1) - (x + 0,6)= -0,2...

Популярные вопросы