8.22. Не вычисляя корней уравнения 3х2 + 8x - 1 = 0, найдите: х1
Х2
1) х + х);
2) х х + x, x ;
3)
Я |
4) x + х).
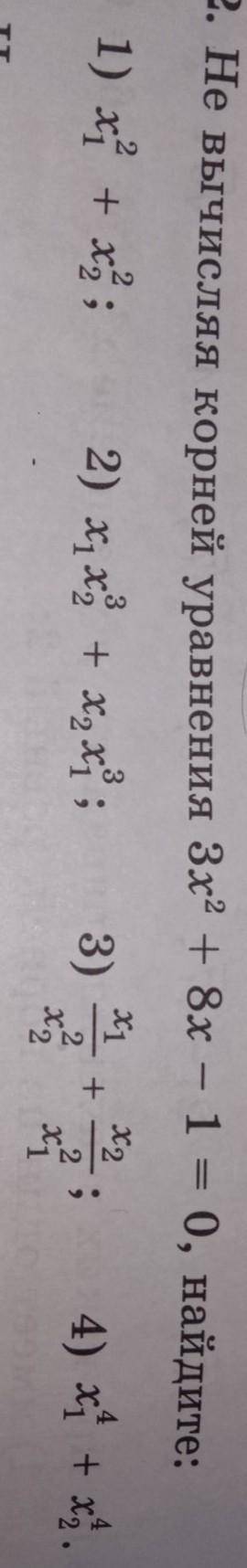
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите сумму всех чисел от -12 до 9...
3 - Поясніть,що таке натуральне господарство...
1 - Карактеризуйте арбуза. 4-5 предложения !...
3 - Влюбом месте между цифрами поставь любые действия и скобки, чтобы получить...
3 - Песня про царя ивана васильевича, молодого опричника и удалого купца калашникова....
2 - Из 280 саженцев 52,5% - яблони, остальные - рябины. сколько рябин?...
2 - Найти угловой коэффициент касательной к графику функции y=f(x) в точке...
1 - Фізика! позначте всі істинні твердження 2 варіанта відповіді. а. температура...
2 - Перездача екзамену, по магазинам, пам ятник шевченка, знати по газетах,...
2 - Написать небольшой рассказ легенду о растегии...
1
Формула для суммы корней уравнения вида ax^2 + bx + c = 0: S = -b/a.
Формула для произведения корней уравнения вида ax^2 + bx + c = 0: P = c/a.
Теперь подставим значения из уравнения 3х^2 + 8x - 1 = 0 в формулы:
S = -(8/3) = -8/3.
P = -(1/3) = -1/3.
Теперь перейдем к заданию:
1) Нам нужно найти значение выражения х + х.
Заметим, что это просто сумма корней уравнения, которая равна -S (так как корни обратно пропорциональны коэффициентам при x в уравнении).
Поэтому, х + х = -(-8/3) = 8/3.
2) Здесь нам нужно найти значение выражения х^2 + х + х, то есть суммы квадратов двух корней плюс сумма двух корней.
По формуле суммы и произведения корней ax^2 + bx + c = 0, это равно (-b/a)(-(-b/a) + 2), то есть S(S + 2).
Подставив значение S = -8/3, получаем S(S + 2) = (-8/3)((-8/3) + 2) = (-8/3)(-8/3 + 6/3) = (-8/3)(-2/3) = 16/9.
3) Здесь нужно найти значение выражения х/(|S| + 1).
Заметим, что значение выражения |S| равно 8/3, поэтому х/(|S| + 1) = х/(8/3 + 1) = х/(8/3 + 3/3) = х/(11/3).
4) В конечном варианте задания нам нужно вычислить выражение х + х.
Мы уже вычислили его в пункте 1: х + х = 8/3.
Таким образом, ответы на задание следующие:
1) х + х = 8/3.
2) х^2 + х + х = 16/9.
3) х/(|S| + 1) = х/(8/3 + 1) = х/(11/3).
4) x + х = 8/3.
Надеюсь, ответ был подробен и понятен для школьника! Если у тебя возникнут еще вопросы, не стесняйся задавать!