74 номер. Завдання з параметром

(см. объяснение)

Объяснение:

Перед нами система из уравнений, графиком каждого из которых является прямая. Применим геометрию и вспомним, что прямые могут пересекаться, совпадать или быть параллельными. В каждом из случаев будет одно решение, их бесконечное множество, отсутствие решений соответсвенно. Нас устраивает первый случай. Опишем его на языке математики, как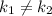 , где 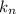- это угловой коэффициент (тангенс угла наклона).

Тогда выразим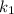 и 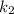из строк исходной системы.

При :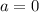

Решением будет пара чисел .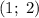

Значит такое значение параметра нам подходит.

При :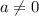

Тогда:

Итого получили, что при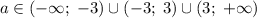 исходная система уравнений имеет ровно одно решение.

Задание выполнено!