72*( 49^1/2log7(9)-log7(6)) + 5^-log sqrt(5) (4) ) решить
Ответы
72*( 49^1/2log7(9)-log7(6)) + 5^-log sqrt(5) (4) )
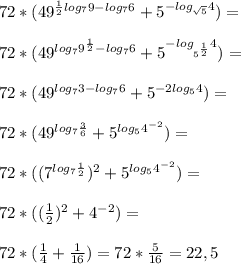
ПОКАЗАТЬ ОТВЕТЫ
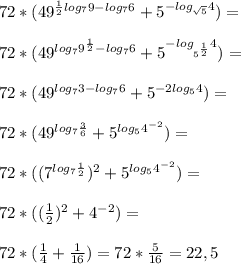
Другие вопросы по теме Алгебра
Популярные вопросы
- с литературой Произведение: Выстрел Почему граф так напуган, тогда...
3 - с задачей сила тока в открытом колебательном контуре изменяется...
2 - 0.04:1.2= скажите ответ с обьеснением)))...
1 - Сколько людей живут в тайге, как в природной зоне...
2 - Напишите миниатюру бессонная ночь 50-80 слов ...
1 - Периметр треугольника CBA равен 45 мм, одна из его сторон равна...
2 - С теоремы Виета найдите значение выражения x21+x22, где x1,x2 –...
2 - -3целые 1/9 :2целые помагите...
3 - Баланс электроэнергии на Аляске ( % вырабатывают ТЭС, ГЭС,АЭС)...
3 - Начертите прямоугольник со стороной А=3см стороной В=4см Найдите...
3