7 гномов очень волнуются за Белоснежку и не пускают её гулять по лесу в одиночестве или в сопровождении только одного гнома, а Белоснежка не хочет огорчать гномов. Сколько существует для Белоснежки: б) выбрать любую подходящую для прогулки компанию гномов? и вторая задача Алфавит цивилизации Набла состоит из пяти букв: а, б, с, в и г. Словом в языке цивилизации Набла может быть любая комбинация из букв их алфавита. б) сколько слов в языке Набла состоит не более чем из четырёх букв и содержит букву г?

1. Белоснежка из семи гномов может выбрать любых двух, любых трех, любых четверых, любых пятерых, любых шестерых или всех семерых. Двух гномов можно выбрать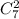 трех - 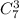и так далее до всех семи гномов, которых можно выбрать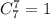

Тогда общее число можно рассчитать непосредственно как сумму:

Можно было воспользоваться интересным свойством для чисел сочетания:

ответ: 120

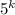2. Рассмотрим ситуацию для слов длины . Всего слов длины можно составить штук (или обозначая через размещения с повторениями 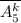). Слов длины , не содержащих букву "г", можно составить 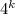штук. Таким образом, слов длины , содержащих букву "г" можно составить штук.

Так как нас интересуют слова, с длиной не более 4 (то есть с длинами 1, 2, 3, 4), то необходимо вычислить следующую сумму:

ответ: 440