(7/8х³у²-5/6ху²)-(-7/12ху²+5/12х³у²)
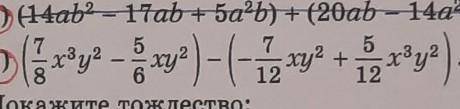
Другие вопросы по теме Алгебра
Популярные вопросы
- Покажите на конкретных примерах, что строение органов дыхания...
1 - Дети шли по дороге. один впереди, двое позади, двое впереди,...
2 - Действие мутантного гена при моногенной патологии проявляется:...
1 - Найдите наибольший общий делитель чисел 32 и 48...
3 - Когда пони был маленьким к нему на день рождения пришли его друзья...
1 - Составить предложение со словами книга...
1 - Когда я был маленьким меня отвезли жить к бабушке.нужен до конца...
1 - Просклонять письменно числа 1981, 1983, 2004...
2 - На каникулы задали провести проект-исследование по предмету на...
2 - Программы сопряжения устройств компьютера называются: a) загрузчиками;...
2
Очень рад, что вы обратились ко мне за помощью в решении этой математической задачи. Позвольте разобрать ее пошагово, чтобы вы смогли легко понять каждую операцию.
Задача заключается в упрощении выражения "(7/8х³у²-5/6ху²)-(-7/12ху²+5/12х³у²)".
1. Начнем с раскрытия скобок: у нас есть два выражения, которые нужно вычесть друг из друга. При этом, второе выражение отрицательное, поэтому, чтобы вычесть его, мы будем менять знаки внутри скобок.
Выражение будет выглядеть так: (7/8х³у²-5/6ху²)+(7/12ху²-5/12х³у²).
2. Теперь сгруппируем подобные слагаемые.
Сначала сложим слагаемые с х³у²: 7/8х³у² + 5/12х³у². Для этого нужно найти общий знаменатель, который является наименьшим общим кратным знаменателей 8 и 12, а это будет 24.
7/8х³у² + 5/12х³у² = (21/24 + 10/24)х³у² = 31/24х³у².
Теперь сложим слагаемые с ху²: -5/6ху² + 7/12ху². В этом случае наименьший общий знаменатель будет 12.
-5/6ху² + 7/12ху² = (-10/12 + 7/12)ху² = -3/12ху².
3. После сгруппирования подобных слагаемых получаем: (31/24х³у²) + (-3/12ху²).
Можно сократить -3/12 на 3/4, так как и 3, и 12 делятся на 3.
Выражение теперь выглядит следующим образом: (31/24х³у²) + (-(3/4)ху²).
4. Теперь суммируем слагаемые в скобках. Обратите внимание на знак "-", который стоит перед вторым слагаемым.
(31/24х³у²) + (-(3/4)ху²) = (31/24х³у² - 3/4ху²).
5. Определим общий знаменатель в этом выражении. Наименьшим общим кратным знаменателей 24 и 4 будет 24.
Выражение примет вид: (31/24х³у² - 18/24ху²).
6. Теперь, когда у нас есть общий знаменатель, мы можем вычесть числители. В данном случае, числитель первого слагаемого является 31/24х³у², а числитель второго -18/24ху².
(31/24х³у² - 18/24ху²) = (31х³у² - 18ху²) / 24.
Итак, итоговый ответ: (31х³у² - 18ху²) / 24.
Это решение является полным и детальным, чтобы школьнику было понятно, как мы пришли к ответу и какие операции выполняли на каждом шаге. Надеюсь, что вы поняли каждый шаг решения и готовы использовать его для решения аналогичных задач в будущем. Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать их. Я всегда рад помочь вам!