Алгебра: 503 и 4 _._._._._._._._._._

3)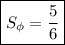 квадратных единиц4)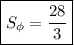 квадратных единицОбъяснение:3)По условию фигура ограничена линиями:Линии ограничивают область (закрашенную желтым цветом и которую можно назвать ABC).Прямые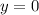 и и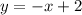меют пересечения в точке C(2;0).0 = -x + 2 ⇒ x = 2; y(-2) = 0Прямые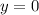 и 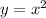имеют пересечения в точке A(0;0).Прямые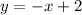 и 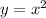имеют пересечения в точке B(0;0).Однако так как нас согласно расположению графиков относительно друг друг друга, то нас интересует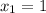 , то есть точка B(1;1).Проведем прямую x = 1. Таким образом она разбила...

50
3 и 4
_._._._._._._._._._

503 и 4 _._._._._._._._._._

Ответы

tanyatanechk 15.02.2022 08:40

3) $\boxed{S_{\phi} = \dfrac{5}{6}}$ квадратных единиц

4) $\boxed{S_{\phi} = \dfrac{28}{3}}$ квадратных единиц

Объяснение:

По условию фигура ограничена линиями:

$y = x^{2}$

y = 0

y = -x + 2

Линии ограничивают область (закрашенную желтым цветом и которую можно назвать ABC).

Прямые y = 0 и y = -x +2 имеют пересечения в точке C(2;0).

0 = -x + 2 ⇒ x = 2; y(-2) = 0

Прямые y = 0 и $y = x^{2}$ имеют пересечения в точке A(0;0).

Прямые y = -x + 2 и $y = x^{2}$ имеют пересечения в точке B(0;0).

$-x + 2 = x^{2}$

$x^{2} + x - 2 = 0$

$D = 1 - 4 \cdot 1\cdot (-2) =1 + 8 = 9 = 3^{2}$

$x_{1} = \dfrac{-1 + 3}{2} = \dfrac{2}{2} = 1$

$x_{2} = \dfrac{-1 -3}{2} = \dfrac{-4}{2} = -2$

Однако так как нас согласно расположению графиков относительно друг друг друга, то нас интересует $x_{1} = 1$ , то есть точка B(1;1).

Проведем прямую x = 1. Таким образом она разбила желтую часть на две фигуры. Где площадь криволинейно трапеции ABD с пределами интегрирования от 0 до 1 можно найти с определенного интеграла, а оставшуюся площадь, как площадь треугольника BDC. То есть площадь фигуры имеет вид: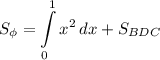 $S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC}$ .

а)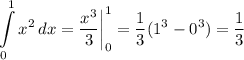 $\displaystyle \int\limits^1_0 {x^{2} } \, dx = \dfrac{x^{3}}{3} \bigg | _0^1 = \dfrac{1}{3}(1^{3} - 0^{3}) = \dfrac{1}{3}$ квадратных единиц.

б)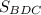 $S_{BDC}$

Так как отрезок BD треугольника ΔBDC лежит на прямой x = 1, то треугольник ΔBCD - прямоугольный с катетами BD и DC.

Зная координаты точек B(1;1),D(1;0),C(2;0) найдем длинны отрезков BD и DC.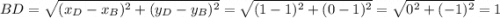 $BD = \sqrt{(x_{D} - x_{B})^{2} + (y_{D} - y_{B})^{2}} = \sqrt{(1 - 1)^{2} + (0 - 1)^{2}} = \sqrt{0^{2} + (-1)^{2}} = 1$ .

$DC = \sqrt{(x_{C} - x_{D})^{2} + (y_{C} - y_{D})^{2}} = \sqrt{(2 - 1)^{2} + (0 - 0)^{2}} = \sqrt{1^{2} + 0^{2}} = 1$ .

По формуле площади прямоугольного треугольника (ΔBDC) :

$S_{BDC} = 0,5 \cdot BD \cdot CD = 0,5 \cdot 1 \cdot 1 = 0,5$ квадратных единиц.

в) Площадь фигуры: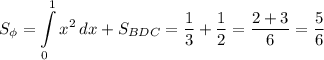 $S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC} = \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{2 + 3}{6} = \dfrac{5}{6}$ квадратных единиц.

По условию фигура ограничена линиями:

$y = 2\sqrt{x}$

y = 0

x = 1

x = 4

Пределы интегрирования:

a = 1

b = 4

Найдем площадь криволинейной трапеции по определению:

$S_{\phi} = \displaystyle \int\limits^4_1 {2\sqrt{x} - 0 } \, dx = \displaystyle 2 \int\limits^4_1 {\sqrt{x} } \, dx = \dfrac{4x\sqrt{x} }{3} \bigg | _4^1 = \dfrac{4}{3} (4\sqrt{4} - 1\sqrt{1)} = \dfrac{4}{3}(4 \cdot 2 - 1 \cdot 1)=$