1. Алгебра
  2. [50 решить систему уравнений:

[50

решить систему уравнений:

{x}^{3} + {y}^{3} = 19 \\ {x}^{2} + xy = - 6

dashakid1 dashakid1    3   19.10.2019 19:16    0

Ответы
lovemopeio lovemopeio  10.10.2020 08:13

Преобразуем первое уравнение: разложим на множители

(x+y)(x^2-xy+y^2)=19\\ (x+y)\Big((x+y)^2-3xy\Big)=19

Из второго уравнения понятно что xy = -6 - x² и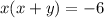 x(x+y)=-6 откуда 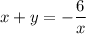x+y=-\dfrac{6}{x}. Подставляем все это в преобразованное уравнение.

-\dfrac{6}{x}\cdot \left(\left(-\dfrac{6}{x}\right)^2-3\cdot (-6-x^2)\right)=19\\ \\ -\dfrac{6}{x}\cdot \left(\dfrac{6}{x^2}+3x^2+18\right)=19~~~~\bigg|\cdot x^3\\ \\ -6x^2\cdot\left(\dfrac{6}{x^2}+3x^2+18\right)=19x^3\\ \\ \\ -36-18x^4-108x^2=19x^3\\ \\ \\ 18x^4+19x^3+108x^2+36=0\\ \\ \\ 18\left(x^2+\dfrac{19}{36}x\right)^2+\dfrac{7415}{72}x^2+36=0

Видим, что левая часть уравнения принимает только положительные значения, а правая - 0, следовательно, уравнение решений не имеет.

ответ: система решений не имеет.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
EkaterinaVNTOGLIATTI EkaterinaVNTOGLIATTI  21.09.2019 22:00
Найдите все первообразные функции f(x)=x^5+2x...
hahausyxu hahausyxu  21.09.2019 22:00
Известно, что график уравнения у=1/3х - 5 проходит через точку в, абцисса которой равна 6. найдите ординату у этой точки...
Svetiksmail5454 Svetiksmail5454  21.09.2019 22:00
Выражение cos 5a + cos 9a ÷ sin 5a + sin 9a....
ASTRA5555 ASTRA5555  21.09.2019 22:00
Найти первообразные а) 5 sin x+2 cos x б) 1+3 e^x -4 cos x в) 4/корень x +3/x -2 e^x...
sodel28 sodel28  21.09.2019 22:00
Aи б были на расстоянии 100 метров друг от друга, и начали движение в одном направлении. а догнал б через 50 секунд, притом что скорость а вдвое больше скорости б. найти...
KristinaSagat55555 KristinaSagat55555  21.09.2019 22:00
3sin в квадрате x- 2sonx· cosx =3cos в квадрате x...
SachaNabok SachaNabok  21.09.2019 22:00
,! огрубление сумм и произведений. чтобы сумма 1 + 1/2+1/3++1/n была больше 1000 достаточно взять: 1)n=1000 2)n=2000 3)n=2⁵⁰⁰ 4)n=2⁹⁹⁸ 5)n=2¹⁰⁰⁰ 6)n=2²⁰⁰⁰ 7)такого n...
fiyyk fiyyk  21.09.2019 22:00
Найти сумму всех двузначных чисел делящихся на 7...
Маша28201 Маша28201  25.05.2020 11:27
8. Звільніться від ірраціональності в знаменнику дробу...
deniskarpov02 deniskarpov02  25.05.2020 11:27
Напишите общее уравнение прямой, проходящей через точку A(5, 2) и перпендикулярной прямой, проходящей через точки B( − 4, 5) и C( − 7, 9) ....

Популярные вопросы