Алгебра: №5. Решите тригонометрическое неравенство.

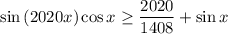
№5. Решите тригонометрическое неравенство. $\sin{(2020x)} \cos{x}\ge \dfrac{2020}{1408} +\sin{x}$

Ответы

Anna19013 15.10.2020 15:26

Заметим, что $\forall x:|\cos x|\geq \sin(2020x)\cos x$ . Теперь рассмотрим два случая:

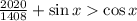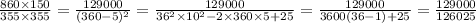1) $\cos x\geq 0$ . Докажем справедливость неравенства $\frac{2020}{1408}+\sin x\cos x$ для всех таких переменных. Заметим, что $\cos x-\sin x=\sqrt{2}\sin(\pi/4-x)\leq \sqrt{2}$ , последнее неравенство получилось следующим образом: возведем обе части неравенства в квадрат и вычтем единицу, получим: , последняя величина больше $\frac{860\times 150}{355\times 355}=\frac{129000}{(360-5)^2}=\frac{129000}{36^2\times 10^2-2\times360\times 5+25}=\frac{129000}{3600(36-1)+25}=\frac{129000}{126025}$ , поэтому больше 1.

2) $\cos x$ . Тогда нужно доказать $\frac{2020}{1408}+\sin x-\cos x$ . Но $\sin x+\cos x=\sqrt{2}\cos(x-\pi/4)\geq -\sqrt{2}-\frac{2020}{1408}$ .

Объединив эти случаи, приходим к неравенству $|\cos x|$ , верному для любого . Итого: $\frac{2020}{1408}+\sin x|\cos x|\geq \sin(2020x)\cos x$ , значит исходное неравенство не выполнено ни при каком