1. Алгебра
  2. 4sinx*cosx*cos2x=sin^2

4sinx*cosx*cos2x=sin^2 4x , решите уравнение,

nikusakunova nikusakunova    2   29.06.2019 22:10    11

Ответы
druwban druwban  02.10.2020 15:39
Преобразуем правую часть использую формулу синуса двойного угла
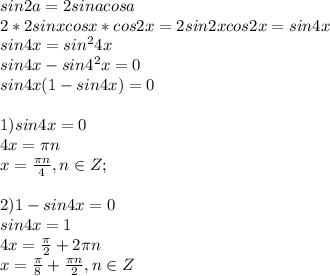
sin2a=2sinacosa \\ 2*2sinxcosx*cos2x=2sin2xcos2x=sin4x \\ sin4x=sin^{2}4x \\ sin4x-sin4^{2}x=0 \\ sin4x(1-sin4x)=0 \\ \\ 1)sin4x=0 \\ 4x=\pi n \\ x= \frac{\pi n}{4},n\in Z; \\ \\ 2)1-sin4x=0 \\ sin4x=1 \\ 4x= \frac{\pi}{2}+2\pi n \\ x= \frac{\pi}{8}+ \frac{\pi n}{2},n\in Z
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
fox02713foxsi fox02713foxsi  17.02.2021 18:41
решить вариант б2 полностью...
pixxxiv pixxxiv  17.02.2021 18:41
уравнение БЛ*ТЬ ЧЕМ КОНТРОХА​...
71121 71121  17.02.2021 18:42
данное положительное число t представьте в виде суммы двух слагаемых так, чтобы их произведение было наибольшим....
Angilass Angilass  13.12.2020 15:39
Выполните умножение многочленов. ​...
далина3 далина3  13.12.2020 15:39
Сколько решений имеет уравнение |x²-2x-4| -4=0...
karinatan12354 karinatan12354  13.12.2020 15:40
Прямые y= ax + 3,5 и 10y + 14x + 35 = 0 пересекаются в точке, принадлежащей оси абсцисс. Найдите a и площадь треугольника, ограниченного этими прямыми и осью ординат....
ksapko ksapko  13.12.2020 15:40
Дана геометрическая прогрессия первый член которой -32, а знаменатель равен 0,5. а) найдите её шестой член б) найдите сумму её первых семи членов...
ostapsheremetaoooo ostapsheremetaoooo  13.12.2020 15:41
Знайдіть область значень функціїдо ть будь ласка ​...
alyamiller1513 alyamiller1513  13.12.2020 15:41
Алгебра лист сделайте отsosу...
artem874 artem874  13.12.2020 15:42
умаляю очень надо! Заранее Упрастите выражение: a) -2ab³·3a²·b⁴ б) (-2a⁵b²)³...

Популярные вопросы