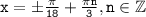4cos^2 6x+ 16 cos^2 3x=13 решить пременяя формулы понижения степени
Другие вопросы по теме Алгебра
Популярные вопросы
- В6 каробках поровну 36 фламастеров. сколько фломастеров в13 каробках?...
3 - Ркiмге өзiнiң туған жер - жерұық деген тұжырым бойынша ой бөлiсiңдер.заранее...
1 - Сочинение на тему: м.м.пришвин писал: какой бы не была погода во дворе,она...
2 - Тело повешено к пружине и находится в равновесии.исполняет ли роботу сила...
3 - Определить рыночную стоимость четырехкомнатной квартиры с двумя санузлами,...
1 - 335 стр 123 по языку 4 класс калюжная и качигулова...
2 - {-2х-0,8у-1=0. {-2х+0,2у=0 {4х-2/3у+3 1/3=0 {4х+3 1/3у-2/3=0 умоляю, (...
3 - Страна-крупнейшая метрополия к началу 20 века? 1-россия 2-сша 3-великобритании...
1 - Найдите неизвестный член пропорции...
3 - Округлите число 4,56784; 456009 до сотых...
3
Во втором слагаемом применим формулу понижения степени, имеем
Решим последнее уравнение как квадратное уравнение относительно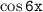
ответ: