473. Найти точки графика функции  , через которые касательные к графику нарисованной функции параллельны оси абсцисс, когда:
, через которые касательные к графику нарисованной функции параллельны оси абсцисс, когда:
b)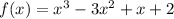
Другие вопросы по теме Алгебра
Популярные вопросы
- Народныйе вотания 11 векаТы лох...
1 - Одно из двухя У чому виявляється багатогранність образу Гобсека?...
2 - Твір роздум на тему Вірність і відданість християнським переконанням...
3 - Подій до оповідання Жага до життя до зарубіжної...
1 - Підкресли використані в перекладі твору Данте засоби художньої...
3 - Сколько грамм кислорода необходимо для получения 5,1 г H2O. я вас...
2 - Разложите на множители: 9x^3 - 36x...
3 - Сколько будет стоить кг яблок если в каждом яшике 150 кг(яшиков10)...
2 - Характеристика Хлестакова из комедии „Ревизор” (10-15 предложений)...
3 - Химия 8 класс до завтра очень нужно...
2
Сначала найдем производную функции f(x). Для этого возьмем производную каждого члена функции и запишем результат:
f'(x) = (x^3)' - (3x^2)' + (x)' + 2'
= 3x^2 - 6x + 1
Теперь приравняем полученную производную к нулю и решим это уравнение для x:
3x^2 - 6x + 1 = 0
Мы можем решить это уравнение с помощью квадратного трехчлена, дискриминанта и формулы квадратного корня. Для решения будем использовать дискриминант D, который равен b^2 - 4ac. В нашем случае a = 3, b = -6, c = 1:
D = (-6)^2 - 4*3*1
= 36 - 12
= 24
Так как D > 0, у нас есть два различных корня (два значения x), которые являются точками графика функции, через которые проходят касательные, параллельные оси абсцисс.
Теперь используем формулу квадратного корня:
x = (-b +/- √D) / 2a
x = (-(-6) +/- √24) / (2*3)
x = (6 +/- √24) / 6
Разделим и упростим эту формулу:
x = (6 +/- 2√6) / 6
x = 1 +/- (√6) / 3
Итак, точки графика функции, через которые проходят касательные, параллельные оси абсцисс, равны:
x1 = 1 + (√6) / 3
x2 = 1 - (√6) / 3
Вы можете использовать значение x1 и x2 для нахождения соответствующих y-координат, подставив их в исходную функцию f(x):
y1 = f(x1) = (x1)^3 - 3(x1)^2 + x1 + 2
y2 = f(x2) = (x2)^3 - 3(x2)^2 + x2 + 2
Итак, чтобы найти точки графика функции, через которые касательные параллельны оси абсцисс для функции f(x) = x^3 - 3x^2 + x + 2, мы должны найти значения x1 и x2, которые мы нашли равными 1 + (√6) / 3 и 1 - (√6) / 3 соответственно. Затем, мы можем найти значения y1 и y2, подставив эти значения x в исходную функцию.