412. Для каждой из функций: а) у = (х – 3)²;
б) у = -(х + 2)²
в) у = 2(x — 1)²;
г)
найдите:
1) вершину параболы; 2) ось симметрии параболы;
3) две точки параболы, симметричные относительно ее оси сим-
метрии; 4) точку пересечения с осью Оy и точку, симметричную
ей относительно оси симметрии параболы, и постройте ее график.
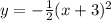
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужна задания по геометрий уровня 8 класса Желательно предоставить ответ с формулами...
2 - Выбери правильный ответ на вопросы которые в карточке...
2 - с математикой надо решить по действиям...
2 - Решите уравнение 1,6y^3-0,4y=0...
3 - Составьте уравнение реакции взаимодействия а) оксида железа 3 с алюминием; б) сульфата...
2 - Первый нитяной маятник совершил за некоторое время 10 колебаний, а второй за то...
2 - 4. Определите местоимение с отрицательной приставкой НЕ-: а) (Н..)перед(кем) не...
3 - Какую оценку поэме Мёртвые души даёт сам Николай Гоголь и его современники?...
2 - Как это делается не понимаю последняя попытка...
2 - Опишите владения Караханидов?...
2
а) Функция у = (х – 3)²:
1) Для нахождения вершины параболы можно использовать формулу x = -b/2a, где a и b - коэффициенты при x^2 и x соответственно. В данной функции a = 1, b = -6 и c = 9 (так как х - 3 = 0, то х = 3).
Теперь найдем x-координату вершины:
x = -(-6)/(2*1) = 6/2 = 3
Подставляем данное значение в функцию, чтобы найти y-координату вершины:
y = (3 - 3)² = 0² = 0
Таким образом, вершина параболы у = (х – 3)² находится в точке (3, 0).
2) Ось симметрии параболы проходит через вершину и является вертикальной линией, которая в данном случае соответствует x = 3.
3) Две точки параболы, симметричные относительно ее оси симметрии можно найти, заменив значение x на значение симметричное относительно оси симметрии.
Например, возьмем точку (2, 1): значение функции для x = 2 будет равно
y = (2 - 3)² = (-1)² = 1, что соответствует точке (2, 1) на параболе.
По аналогии найдем вторую точку, симметричную относительно оси симметрии. Пусть, например, x = 4:
y = (4 - 3)² = (1)² = 1, что соответствует точке (4, 1) на параболе.
4) Точку пересечения с осью Оy можно найти, подставив x = 0 в функцию:
y = (0 - 3)² = (-3)² = 9
Точка пересечения с осью Оy равна (0, 9). Чтобы найти точку, симметричную ей относительно оси симметрии параболы, достаточно заменить знак у координаты x:
(-1) * (0) = 0, значит, точка (0, -9) будет симметричной точкой.
Построим график функции у = (х – 3)²:
[graph]
б) Функция у = -(х + 2)²:
1) Найдем вершину параболы:
a = -1, b = -4 и c = -4 (так как х + 2 = 0, то х = -2).
x = -(-4)/(2*(-1)) = 4/-2 = -2
y = -(-2 + 2)² = -(0)² = 0
Вершина параболы у = -(х + 2)² находится в точке (-2, 0).
2) Ось симметрии параболы проходит через вершину и является вертикальной линией, которая в данном случае соответствует x = -2.
3) Две точки параболы, симметричные относительно ее оси симметрии можно найти, заменив значение x на значение симметричное относительно оси симметрии.
Например, возьмем точку (0, -4): значение функции для x = 0 будет равно
y = -(0+2)² = -(2)² = -4, что соответствует точке (0, -4) на параболе.
По аналогии найдем вторую точку, симметричную относительно оси симметрии. Пусть, например, x = -4:
y = -(-4+2)² = -(6)² = -36, что соответствует точке (-4, -36) на параболе.
4) Точку пересечения с осью Оy можно найти, подставив x = 0 в функцию:
y = -(-2 + 2)² = 0
Точка пересечения с осью Оy равна (0, 0). Чтобы найти точку, симметричную ей относительно оси симметрии параболы, достаточно заменить знак у координаты x:
-(-2) = 2, значит, точка (2, 0) будет симметричной точкой.
Построим график функции у = -(х + 2)²:
[graph]
в) Функция у = 2(x - 1)²:
1) Найдем вершину параболы:
a = 2, b = -4 и c = 2 (так как x - 1 = 0, то x = 1).
x = -(-4)/(2*2) = 4/4 = 1
y = 2(1 - 1)² = 2*0² = 0
Вершина параболы у = 2(x - 1)² находится в точке (1, 0).
2) Ось симметрии параболы проходит через вершину и является вертикальной линией, которая в данном случае соответствует x = 1.
3) Две точки параболы, симметричные относительно ее оси симметрии можно найти, заменив значение x на значение симметричное относительно оси симметрии.
Например, возьмем точку (0, 2): значение функции для x = 0 будет равно
y = 2(0 - 1)² = 2*(-1)² = 2, что соответствует точке (0, 2) на параболе.
По аналогии найдем вторую точку, симметричную относительно оси симметрии. Пусть, например, x = 2:
y = 2(2 - 1)² = 2*(1)² = 2, что соответствует точке (2, 2) на параболе.
4) Точку пересечения с осью Оy можно найти, подставив x = 0 в функцию:
y = 2(0 - 1)² = 2*(-1)² = 2
Точка пересечения с осью Оy равна (0, 2). Чтобы найти точку, симметричную ей относительно оси симметрии параболы, достаточно заменить знак у координаты x:
-(-1) = 1, значит, точка (1, 2) будет симметричной точкой.
Построим график функции у = 2(x - 1)²:
[graph]
г) Функция y = -1/2 (x + 3)²:
1) Найдем вершину параболы:
a = -1/2, b = -3 и c = -9 (так как x + 3 = 0, то x = -3).
x = -(-3)/(2*(-1/2)) = 3/(1) = 3
y = -1/2((-3) + 3)² = -1/2(0)² = -1/2*0 = 0
Вершина параболы y = -1/2 (x + 3)² находится в точке (-3, 0).
2) Ось симметрии параболы проходит через вершину и является вертикальной линией, которая в данном случае соответствует x = -3.
3) Две точки параболы, симметричные относительно ее оси симметрии можно найти, заменив значение x на значение симметричное относительно оси симметрии.
Например, возьмем точку (0, -9/2): значение функции для x = 0 будет равно
y = -1/2(0+3)² = -1/2(3)² = -1/2*9 = -9/2, что соответствует точке (0, -9/2) на параболе.
По аналогии найдем вторую точку, симметричную относительно оси симметрии. Пусть, например, x = -6:
y = -1/2((-6)+3)² = -1/2*(-3)² = -1/2*9 = -9/2, что соответствует точке (-6, -9/2) на параболе.
4) Точку пересечения с осью Оy можно найти, подставив x = 0 в функцию:
y = -1/2(0 + 3)² = -1/2(3)² = -1/2*9 = -9/2
Точка пересечения с осью Оy равна (0, -9/2). Чтобы найти точку, симметричную ей относительно оси симметрии параболы, достаточно заменить знак у координаты x:
-(-3) = 3, значит, точка (3, -9/2) будет симметричной точкой.
Построим график функции y = -1/2 (x + 3)²:
[graph]
Надеюсь, мой ответ был понятен. Если у вас остались вопросы, обращайтесь!