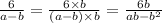4. Зведіть дроби до нових знаменників:

Другие вопросы по теме Алгебра
Популярные вопросы
- В чем главная причина броуновского движения? Почему ваше тело не совершает...
3 - 5 класс математика номер 221 Никольский купили 60 тетрадей, причем тетрадей...
3 - Hа згоряння 0,5 моль алкену витратили 33,6л кисню (н.у.) становити формулу...
2 - Слово заутра это историзмы или архаизмы...
3 - каждому слову подберите зависимые Запишите полученные словосочетания Укажите...
3 - Укажите неверное утверждение * 1) деепричастия не изменяются2) деепричастие...
1 - а то мозги не шарят заболела. Мне 2 и 3...
2 - для каждого числа процентов из верхней строки укажите соответствующию...
2 - Є відомості про зріст кожного учня та учениці вашого класу. Обчисліть...
1 - Как и во сколько раз изменится ускорение движения тела а, если действующая...
1
Разделим новый знаменатель на старый, чтобы узнать на сколько нужно умножить дробь.
Итак, Б
В
В А есть ошибка. Довести дробь до такого знаменателя не получается.
1) Либо дробь должна быть такой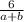
Тогда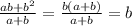
И получается,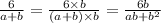
2) Либо новый знаменатель должен быть таким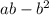
Тогда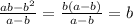
И получается,