Алгебра: (4-cos^2x-3)/sqrt(cosx) = 0

(4-cos^2x-3)/sqrt(cosx) = 0

Ответы

zhenya4546 11.10.2020 06:23

На множестве действительных чисел:

$x = 2\pi k, \: k \in \mathbb{Z}$

На множестве комплексных:

$x = \pi n, \: n \in \mathbb{Z}$

Задание, скорее всего из ЕГЭ (№13, уравнение), а значит рассматриваем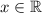 $x \in \mathbb{R}$ , т.е. правильный первый ответ.

Объяснение:

Если решать только в области действительных чисел, то:

Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю и существует, значит:

$\frac{4 - \cos^{2}(x) - 3}{ \sqrt{ \cos(x) } } = 0 \\ \Downarrow \\ \left \{{4 - \cos^{2}(x) - 3 = 0} \atop { \sqrt{ \cos(x)} \ne 0} \right. \\ \left \{{\cos^{2}(x) = 1} \atop { \cos(x) 0} \right. \\ \left \{{ \cos(x) = 1 \: or \: \cos(x) = - 1 } \atop { \cos(x) 0} \right. \\ \Downarrow \\ \cos(x) = 1 \\ x = 2\pi k, \: k \in \mathbb {Z}$

А если решать, учитывая и комплексные корни, то:

$\frac{4 - \cos^{2}(x) - 3}{ \sqrt{ \cos(x) } } = 0 \\ \Downarrow \\ \left \{{4 - \cos^{2}(x) - 3 = 0} \atop { \sqrt{ \cos(x)} \ne 0} \right. \\ \left \{{\cos^{2}(x) = 1} \atop { \cos(x) \ne 0} \right. \\ \left \{{ \cos(x) = 1 \: or \: \cos(x) = - 1 } \atop { \cos(x) \ne 0} \right. \\ \Downarrow \\ \cos(x) = 1 \: or \: \cos(x) = -1 \\ x = 2\pi n_{1}, \: n_{1} \in \mathbb {Z} \: or \: x= \pi + 2\pi n_{2}, \: n_{2} \in \mathbb{Z} \\ \Downarrow \\ x = \pi n, \: n \in \mathbb{Z}$