1. Алгебра
  2. 4.1 завдання з параметрами,

4.1 завдання з параметрами, 11 клас


4.1 завдання з параметрами, 11 клас

mika181minecrafMilka mika181minecrafMilka    1   10.07.2021 20:55    0

Ответы
agasan420 agasan420  09.08.2021 21:35

(см. объяснение)

Объяснение:

\sin^2x-\left(a+\dfrac{1}{2}\right)\sin x+\dfrac{a}{2}=0

Выполним временную замену вида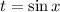 t=\sin x.

t^2-\left(a+\dfrac{1}{2}\right)t+\dfrac{a}{2}=0

Попробуем решить это уравнение через дискриминант относительно неизвестной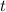 t.

D=\left(a+\dfrac{1}{2}\right)^2-4\times\dfrac{a}{2}=a^2-a+\dfrac{1}{4}=\left(a-\dfrac{1}{2}\right)^2

\sqrt{D}=a-\dfrac{1}{2}

\left[\begin{array}{c}t=a\\t=\dfrac{1}{2}\end{array}\right;

Сделаем обратную замену:

\left[\begin{array}{c}\sin x=a\\\sin x=\dfrac{1}{2}\end{array}\right;

Второе уравнение совокупности дает нам два корня, принадлежащие промежутку \left[0;\;\dfrac{5\pi}{4}\right]. Значит надо, чтобы первое давало один.

Здесь графическое решение на единичной окружности:

(см. прикрепленный файл)

Итого при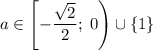 a\in\left[-\dfrac{\sqrt{2}}{2};\;0\right)\cup\left\{1\right\} исходное уравнение имеет ровно три различных корня.

Задание выполнено!


4.1 завдання з параметрами, 11 клас
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
GoodArtur GoodArtur  22.08.2019 19:50
20 . найдите значение одночлена: 3а²b, при а = 2, b = -1...
gadazak gadazak  22.08.2019 19:50
Найдите первый член прогрессии,если ивестны ее знаменатель d и третий член 1)q=4/3; b3=64 2)q=-2/3,b3=8,1...
dary090 dary090  22.08.2019 19:40
9k−42−9k +∗2−9k =1 вместо ∗ запиши такое выражение, чтобы получилось верное равенство....
busiginanst99 busiginanst99  22.08.2019 19:40
Площадь треугольника,основание которого на 20 см. больше высоты,равна 78 см. в кв.найдите основание треугольника....
adonnush adonnush  22.08.2019 19:40
Если сложить 10 натуральных чисел, получится 20; если перемножить - тоже 20. что это за числа? ? 15...
вика2832 вика2832  22.08.2019 19:40
Составить схему и решить . в зоопарке было 12 курапаток, 15 глухарей, а тетеревов столько, сколько курапаток и глухарей вместе. сколько тетеревов было в зоопарке...
arina88561 arina88561  22.08.2019 19:40
(5-d)^3+(5-t)(t+2)+(5-t)(t-11)решите...
svetbuxzp51 svetbuxzp51  22.08.2019 19:40
За 5 компьютеров и 3 одинаковых ксерокса организация выплатила 210000р.цена каждого компьютера 30000 р.сколько стоит один ксерокс?...
kokocuk01 kokocuk01  23.12.2020 20:40
‼️Геометрия ‼️ 3) Окружность задана уравнением: (х+2)в квадрате + (у-5) в квадрате =18. Принадлежит ли этой окружности точка M(-5;2)? завтра кр, времени нет(​...
pasatnuk pasatnuk  23.12.2020 20:40
16-летний школьник хочет устроится на работу, где ему за 1 час будут платить 200 рублей. При этом он хочет 1 раз ходить в кино, где билет в кино стоит 200 рублей, есть не меньше 4...

Популярные вопросы