㏒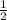 (3x-1)≤-2 если что то там логарифм (3x-1) по основанию 1/2
(3x-1)≤-2 если что то там логарифм (3x-1) по основанию 1/2
Решить логарифмическое неравенство с объяснением.
Другие вопросы по теме Алгебра
Популярные вопросы
- Хто багато знає тот наполеглево працює звук опис...
2 - Найти сумму четных элементов массива из 10 чисел случайных, отрезка [15..30]...
1 - Новостях передавали Чили произошло землетрясение силой по шкале рихтера какую...
1 - , Физика 7 класс ,§19 автор:Л.А.Исаченкова и Ю.Д.Лещинский Вопросы номер 3...
2 - твір на одну із тем: Наша слава- козацька звитяга за твором В.Рутківського...
3 - 1.Choose the correct tense.Dan looked really sunburnt. He in the sun for too...
3 - Мы создали фейк Гитлера в дискорде. Как нужно себя вести, чтобы убедить всех,...
2 - Знайти сім інших кутів за малюнком...
1 - Вписанные и описанные окружности в правильный многоугольник...
1 - Камень бросили с некоторой высоты со скоростью v0, направленной под углом...
2
Объяснение: