35 !
! 7 класс. многочлены

5. докажите, что x^2 + x^2*y^2 + y^2 + 1 является составным числом при любых натуральных x, y.
6. докажите, что 2019^2 + 2020^2 · 2019^2 + 2020^2 является квадратом целого числа.

5.

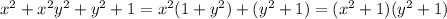
Поскольку x и y - натуральные числа,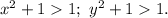

Следовательно, произведение этих чисел является составным числом.

6. Заметим, что 2020=2019+1. Будем решать задачу в более общем виде. А именно, докажем, что при любом целом a выражение

является квадратом целого числа. Имеем: