35.53(2)
Доказать тождество
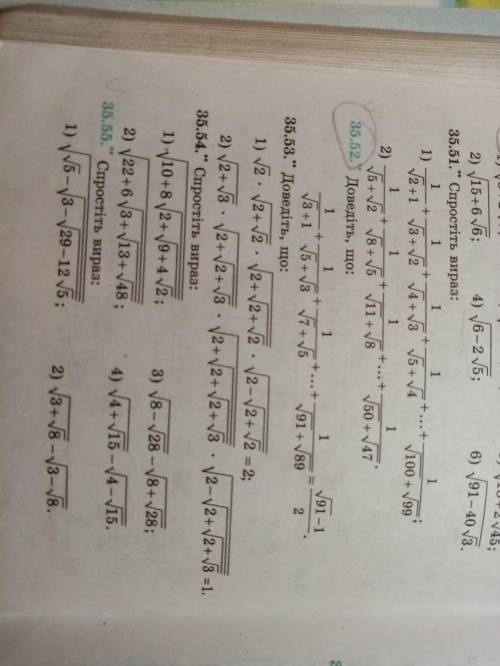
Другие вопросы по теме Алгебра
Популярные вопросы
- Как сделать предложение со словом учитель и в винительном падеже и в именительном...
2 - Спишите расставляя пропущенные запятые и вставляя на месте пропусков зависимые от...
1 - Решите столбиком: a)30 970: 38 б)142 593: 33...
3 - Найди слова в слове и запиши. электровоз и этажерка...
2 - Какое максимальное количество квадратов можно получить нарисовать два прямоугольника...
1 - Умиши значков в 5 раз меньше чем у коли и в 3 раза меньше чем у пети. сколько значков...
1 - Слова с корнем, суффиксом и окончанием...
1 - Какое количество денег барин отдавал за быка и коня в драме барин ?...
3 - 1)какое кол-во теплоты необходимо для нагревания от 10 градусов с до 110 градусов...
3 - Организованная взаимосвязь специализированных предприятий...
1
a² - b² = (a - b)(a + b)
√(2 + √3)*√(2 + √(2 + √3))*(√2+√(2 + √(2 + √3)))*(√2-√(2 + √(2 + √3))) = ...
(√2+√(2 + √(2 + √3)))*(√2-√(2 + √(2 + √3))) = (√2²-√(2 + √(2 + √3))²) = √(4 - 2 - √(2 + √3)) = √(2 - √(2 + √3))
√(2 - √(2 + √3))*√(2 - √(2 + √3)) = √(2² - √(2 + √3)²) = √(4 - 2 - √3) = √(2 - √3)
√(2 - √3)*√(2 - √3) = √(2² - √3²) = √(4 - 3) = 1
= 1