32.19. 1) x(x - 5) - (x - 3)2 <0; 3) (17 - y)> y(y - 13) - 5;
2) (4 + y)2 - y(6 + y)>0;
4) 2(z – 10)>(3 - 2)2.
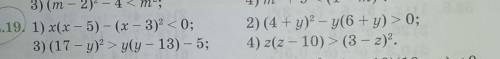
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите сумму всех элементов массива B(N,N), заполненного случайными...
2 - 2. ПРО ДУЛАТОВА Проанализируйте роль и деятельность одного из...
1 - Макс, Катя и Саша насчитали вместе 200 звёзд. Саша насчитал на...
2 - Укажите строку, в которой во всех словах на месте пропусков пишется...
3 - Переведите на немецкий язык. 1. Я учу немецкий язык, потому что...
1 - ФИЗИКА Какую частицу атому легче приобрести – протон или электрон?...
1 - написать текст по вопросам...
2 - Қазақстан Тарихынан Т.Ж.Б 2-тоқсан 5-сынып...
1 - Період ослаблення центральної влади у феодальних державах. А....
1 - Решите уравнение: (11 2/11+y)-5 4/11=8 8/11...
2
1) Решим неравенство x(x - 5) - (x - 3)^2 < 0:
Сначала раскроем скобки:
x^2 - 5x - (x^2 - 6x + 9) < 0.
Упростим выражение:
x^2 - 5x - x^2 + 6x - 9 < 0.
Сократим подобные члены:
x +x - 5x + 6x - 9 < 0.
Объединим члены:
2x - 9 < 0.
Теперь решим получившееся уравнение:
2x < 9.
Разделим обе части неравенства на 2:
x < 9 / 2.
Ответ: x < 4.5.
2) Решим неравенство (4 + y)^2 - y(6 + y) > 0:
Раскроем скобки:
(16 + 8y + y^2) - (6y + y^2) > 0.
Сократим подобные члены:
16 + 8y + y^2 - 6y - y^2 > 0.
Упростим выражение:
16 + 2y > 0.
Вычтем 16 из обеих частей неравенства:
2y > -16.
Разделим обе части неравенства на 2:
y > -8.
Ответ: y > -8.
3) Решим неравенство (17 - y) > y(y - 13) - 5:
Раскроем скобки:
17 - y > y^2 - 13y - 5.
Упростим выражение:
17 - y > y^2 - 13y - 5.
Перенесем все члены в одну часть неравенства:
y^2 - 12y - 22 < 0.
Теперь решим получившееся квадратное уравнение:
Для начала найдем его корни. Воспользуемся формулой дискриминанта:
D = b^2 - 4ac, где a = 1, b = -12, c = -22.
D = (-12)^2 - 4 * 1 * (-22) = 144 + 88 = 232.
Так как D > 0, то уравнение имеет два корня.
Далее найдем сами корни:
y = (-b ± √D) / 2a.
y1 = (-(-12) + √232) / 2 = (12 + 2√58) / 2 = 6 + √58.
y2 = (-(-12) - √232) / 2 = (12 - 2√58) / 2 = 6 - √58.
Теперь построим таблицу знаков:
|(-∞, 6 - √58)| (6 + √58, +∞).
В данном случае используется интервальная нотация, которая показывает, что неравенство выполняется для всех значений y, находящихся в указанных интервалах.
Ответ: (-∞, 6 - √58) и (6 + √58, +∞).
4) Решим неравенство 2(z - 10) > (3 - 2)^2:
Раскроем скобки:
2z - 20 > 1.
Добавим 20 к обеим частям неравенства:
2z > 21.
Разделим обе части неравенства на 2:
z > 21 / 2.
Ответ: z > 10.5.
Итак, решение каждой задачи выглядит следующим образом:
1) x < 4.5.
2) y > -8.
3) y ∈ (-∞, 6 - √58) U (6 + √58, +∞).
4) z > 10.5.
Надеюсь, ответ был понятен. Если возникнут еще какие-либо вопросы, не стесняйтесь задавать их. Я с радостью помогу!