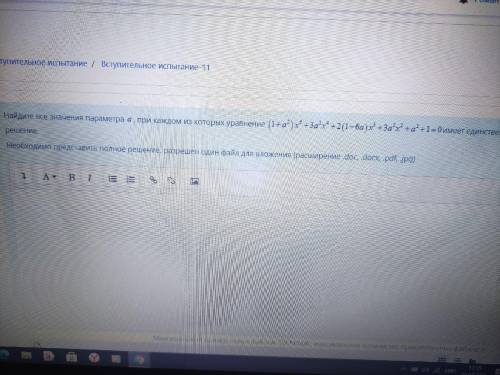
. 30б. Найдите все значения параметра а
Другие вопросы по теме Алгебра
Популярные вопросы
- Выберите правильный ответ: соотнесите между собой названия гипотез социологического...
3 - На примере романа трудно быть богом расскажите, какие серьезные вопросы раскрывают...
1 - Валфавите племени ау есть всего 2 буквы. а и у. причем этот язык обладает...
3 - 0.25×|y+1|=2,5 как решить это уровнение...
1 - Постройте график уравнения; 1) xy=3, 2) xy=-3, 3) x(y-2)=-3, 4) (x+1)(y-2)=3....
3 - Перевод текста the reading public by s. leacock на...
3 - Воздействие на политическую сферу + примеры...
1 - 3. допишите термин выполнения машинных работ: «закрепить подогнутый край...
2 - Подберите однокореные слова разных частей речи -ход- мост-...
1 - Скакой целью ведется реестр хозяйствующих субъектов, имеющие на рынке долю...
3
(см. объяснение)
Объяснение:
Заметим, что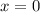 не является корнем уравнения.
не является корнем уравнения.
Тогда поделим его на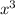 :
:
Выполним группировку:
Заметим, что если - корень уравнения, то
- корень уравнения, то  тоже.
тоже.
Тогда единственное решение возможно, если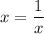 .
.
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда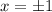 .
.
Подставляя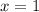 в исходное уравнение, получаем, что
в исходное уравнение, получаем, что 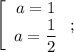
Подставляя , получаем, что
, получаем, что 
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при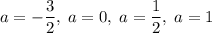 исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!