1. Алгебра
  2. 30 ! умоляю, ! не понимаю, как

30 ! умоляю, ! не понимаю, как решить.
только верно решите, ибо если не знаете как, то не отвечайте, за понимание.
(желательно с объяснением, что да как)​

maksalina2 maksalina2    3   26.01.2020 16:39    0

Ответы
Lizka213 Lizka213  11.10.2020 03:20

ctga=8\\\\\frac{sin(\frac{13\pi }{2}-a)-ctg(6\pi +a)}{1+sin(2\pi -a)}=\frac{sin(6\pi +\frac{\pi}{2}-a)-ctga}{1+sin(-a)}=\frac{sin(\frac{\pi}{2}-a)-8}{1-sina}=\frac{cosa-8}{1-sina} =A\\\\\star\; \; 1+ctg^2a=\frac{1}{sin^2a}\; \; \to \; \; sin^2a=\frac{1}{1+ctg^2a}=\frac{1}{1+8^2}=\frac{1}{65}\; ,\\\\sina=\pm \frac{1}{\sqrt{65}}\\\\cos^2a=1-sin^2a=1-\frac{1}{65}=\frac{64}{65}\; \; \to \; \; \; cosa=\pm \frac{8}{\sqrt{65}}\; \; \star

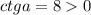Если   ctga=80  , то угол принадлежит 1 или 3 четвертям. Тогда либо sina>0 и cosa>0 (в 1 четверти), либо  sina<0 и cosa<0 (в 3 четверти).

Вычислим значение выражения А в обоих случаях.

1.\; \; A=\frac{cosa-8}{1-sina}=\frac{\frac{8}{\sqrt{65}}-8}{1-\frac{1}{\sqrt{65}}}=\frac{8-8\sqrt{65}}{\sqrt{65}-1}=\frac{8\cdot (1-\sqrt{65})}{-(1-\sqrt{65})}=\frac{8}{-1}=-8\\\\2.\; \; A=\frac{cosa-8}{1-sina}=\frac{-\frac{8}{\sqrt{65}}-8}{1+\frac{1}{\sqrt{65}}}=\frac{-8-8\sqrt{65}}{\sqrt{65}+1}=\frac{-8\cdot (1+\sqrt{65})}{1+\sqrt{65}}=-8

ответ:   -8 .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tatarchenko04 tatarchenko04  12.03.2019 14:33
По представьте в виде многочленов 33.1-33.4 33.2(5-8)​...
котикДжеек котикДжеек  12.03.2019 14:30
Решите 3cosa+4sina/cosa-2sina, если ctga=3​...
dilinur15 dilinur15  03.03.2019 18:26
Даше надо подписать 555 открыток. ежедневно она подписывает на одно и то же количество открыток меньше по сравнению с предыдущим днём. известно, что за первый день даша...
karrtavaya01 karrtavaya01  03.03.2019 18:26
Катер за 2 часа км против течения и 30км по течению ре ки . если б он против течения 10км , а по течению- 42км , тогда он затратил бы на это 2ч30мин . найти скорость катера...
stasyaukg stasyaukg  03.03.2019 18:26
Найдите значение выражения 2корень 13*5корень2*26вкорне​...
Алексаднр Алексаднр  03.03.2019 18:24
Решите уравнение! ! ! заранее​...
annatokar031 annatokar031  03.03.2019 18:23
Иследования проведенные в одной крупной производственной компании показали что производительность труда в течении рабочего времени меняется в зависимости от времени работы...
mahachkala1 mahachkala1  03.03.2019 18:23
Будь ласка розв яжіть номер...
NeTop4ek NeTop4ek  03.03.2019 18:23
(4x в квадрате -1)(9 x в кубе + в кубе -1)в квадрате...
vladkunets78 vladkunets78  03.03.2021 15:14
Какие уравнения задаю ту же прямую что и уравнение 2x-3x =-6​...

Популярные вопросы