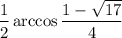30. найти значение выражения (1+17)cos 2x , где хо — наимень-
ший положительный корень уравнения 2sin² x+cos 4x -2 = 0.
Другие вопросы по теме Алгебра
Популярные вопросы
- Сократить дробь на наибольший общий делитель числителя и знаменатель...
1 - Сохраняется ли единство времени в произведении ревизор? почему?...
1 - Напиши слова с поставками. укажи приставки и корни. про...
2 - Какое количество электронов проходит через электрический звонок за...
3 - Решите, , с объяснением. доказать, что значение выражения 27^5 - 9^6...
2 - Что такое теория чистого искусства своими словами?...
2 - Решите уравнение с решением x^5-x^3=0...
3 - Найти значения выражение 50+(9+11) 100-(37-7)...
2 - Начертить ломаную abcd так что бы отрезок cd был больше отрезка ab...
2 - Вначале учебного года в школе было 1250 учащихся, а к концу года...
2
Решаем как квадратное уравнение относительно cos2x
Наименьший положительный корень будет при n = 0 равны