30 !
2. довести, що рівняння
(х-а)(х-в)+(х-в)(х-с)+(х-с)(х-а)=0
завжди має дійсні корені.

Question

Алгебра: 30 ! 2. довести, що рівняння (х-а)(х-в)+(х-в)(х-с)+(х-с)(х-а)=0 завжди має дійсні корені.

bissimbayevaa · Answer

Если уравнение имеет одинаковые корни, то при x = a = b = c выражение равно нулю. Если же имеет различные корни, то обозначим левую часть уравнения через функцию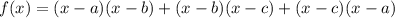 f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)

$f(a)=(a-b)(a-c)\\ f(b)=(b-c)(b-a)\\ f(c)=(c-a)(c-b)\\ f(a)f(b)f(c)=(a-b)(a-c)(b-c)(b-a)(c-a)(c-b)=-(a-b)^2(a-c)^2(b-c)^2$

Т.е. в произвольной точке функция f(x) отрицательная. Квадратичная функция f(x) представляет собой параболу с ветвями направлены вверх и обязательно пересечет ось ОХ, т.е. уравнение имеет корни.

30 ! 2. довести, що рівняння (х-а)(х-в)+(х-в)(х-с)+(х-с)(х-а)=0 завжди має дійсні корені.

Популярные вопросы

30 !
2. довести, що рівняння
(х-а)(х-в)+(х-в)(х-с)+(х-с)(х-а)=0
завжди має дійсні корені.