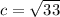30 1. две стороны треугольника равны 10 см и 12 см, а угол между ними — 120°. найдите третью сторону треугольника и его площадь. 2. в треугольнике abc известно, что ac = 5корень2 см, уголb = 45°, уголc = 30°. найдите сторону ab треугольника. 3. определите, остроугольным, прямоугольным или тупоугольным является треугольник со сторонами 6 см, 8 см и 11 см. 4. одна сторона треугольника на 3 см меньше другой, а угол между ними равен 60°. найдите периметр треугольника, если его третья сторона равна 7 см. 5. найдите радиус окружности, вписанной в треугольник со сторонами 4 см, 13 см и 15 см. 6. стороны треугольника равны 4 см, 5 см и 7 см. найдите медиану треугольника, проведённую к его меньшей стороне.

Ответы

rustik1619 09.10.2020 05:31

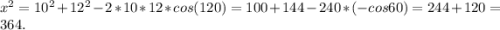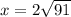
1) По теореме косинусов x^2=10^2+12^2-2*10*12*cos(120)=100+144-240*(-cos60)=244+120=364. ; $x=2\sqrt{91}$

$S=\frac{1}{2}*10*12*sin(120)= 30\sqrt{3}$

2) По теореме синусов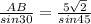 $\frac{AB}{sin30}= \frac{5\sqrt{2}}{sin45}$ ; AB=5.

3) Из теоремы косинусов следует, что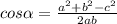 $cos\alpha =\frac{a^2+b^2-c^2}{2ab}$ Пусть напротив стороны длиной 6 см лежит угол α, напротив отрезка длиной 8 см лежит угол 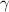$\gamma$ , а напротив стороны длиной 11 см лежит угол β.

Тогда cosα=(8^2+11^2-6^2)/(2*8*11)= 149/176. Значит, α - острый угол.

cosγ=(6^2+11^2-8^2)/(2*6*11)= 93/132

Следовательно,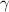 $\gamma$ -острый угол.

Аналогично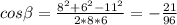 $cos\beta=\frac{8^2+6^2-11^2}{2*8*6}=- \frac{21}{96} \\$ <0 Значит, β - тупой угол.

Таким образом, треугольник - тупоугольный.

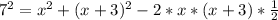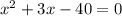4) Пусть треугольник имеет стороны x, x+3 и 7, где угол между сторонами x и x+3 равен 60. По теореме косинусов $7^2=x^2+(x+3)^2-2*x*(x+3)*\frac{1}{2}$ . Выходит, что x^2+3x-40=0 ;

x=-8 или x=5. Значит, x=5. Тогда периметр треугольника равен 5+(5+3)+7=20 см.

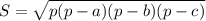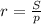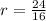5) Пусть a=4 см, b=13 см и c=15 см. Найдем площадь треугольника по формуле Герона. $S=\sqrt{p(p-a)(p-b)(p-c)}$ , где p-полупериметр треугольника. Тогда p=16 см и $S=\sqrt{16*12*3*1}$ =24. Радиус вписанной окружности можно найти по формуле $r=\frac{S}{p}$ . Тогда $r=\frac{24} {16}$ =1,5.

6) Пусть медиана к стороне длиной 4 см равна с. Достроим треугольник до параллелограмма с диагоналями равными 4 и 2*с.

В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон. Докажем этот факт. Ясно, что с^2=a^2+b^2-2*a*b*cosα. Аналогично d^2=a^2+b^2-2*a*b*cos(180α)=a^2+b^2+2*a*b*cosα. Сложим полученные равенства. Выходит, что c^2+d^2=2(a^2+b^2), ч.т.д.

Тогда имеем: 2*(5^2+7^2)=(2*c)^2+4^2

Решив это уравнение получим, что $c=\sqrt{33}$