3. Розв'язати систему рівнянь: {x-y= 3, (x² - xy - 2y² = 7.
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить с формул используя закон сохранения энергии: на какую высоту человек...
1 - Тело, поднятое над столом обладает энергией...
1 - Ссочинением на тему ,,хабар телеагенсттiгi...
1 - Морфологический разбор слова предков...
1 - Три сопротивлениями r1=4ом, r2=5ом и r3=6oм соеденены последовательно и включены...
2 - 1) три тела одинакового объема погрузили в одну и ту же жидкость. первое тело...
3 - Смешали некоторое количество 20-процентного раствора некоторого вещества с...
1 - Выпишите грамматическую основу предложения 2 2) их нужно было внести за обучение...
3 - 1)работа выхода электрона из цепи 1,9 эв. определить максимальную длину волны...
1 - Игральную кость подбрасывают 8 раз. найти вероятность того, что три очка выпадут...
3
(5; 2), (2,5; –0,5)
Объяснение:
Выразим из первого уравнения системы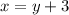 и подставим это выражение во второе уравнение:
и подставим это выражение во второе уравнение:
Тогда