3. Последовательности заданы несколькими первыми членами. [6] Укажите для каждой последовательности соответствующее ей утверждение: 1) Последовательность является арифметической прогрессией. 2) Последовательность является геометрической прогрессией. 3) Последовательность не является ни арифметической, ни геометрической прогрессией. Обоснуй свой ответ. 1; 2; 4; 8;… - 1; 3; 5; 7;… - 1; 8; 27; 64;…
Другие вопросы по теме Алгебра
Популярные вопросы
- Listening Task 2. Listen and complete the text about reality TV shows...
2 - электрон ускоренный разностью потенциалов 6 киловатт влетает в однородное...
3 - Согласны ли вы с позицией автора данного отрывка Приведите не менее...
3 - Уявіть, що ви член середньовічного цеху, розкажіть про нього детальніше,...
3 - Вытачаемое 60 значение разности 35...
3 - Совместный лад И и духовный свет в давних евреев...
1 - Усі вершини квадрата (рис. 48), діа- гональ якого дорівнює 6 см, лежать...
1 - КАк решить задачу по географии ,про матроскина который отпровлялся...
1 - 1. Опишите по карте расположение детского частое Расскажите о его...
1 - ответьие на вопросы 1.какие слои населения Пирненейского полуострова...
2
Можно заметить, что общий член заданной последовательности имеет вид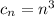 .
.