3. n-ый член арифметической прогрессии выражен формулой
а)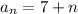
b)
c)
1) является ли число 26 членом этой прогрессии?
2) рассчитайте отличие прогрессии d и 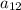
3) рассчитайте сумму первых 28ех членов прогрессии
Другие вопросы по теме Алгебра
Популярные вопросы
- Match the sentences to the objects. Some sentences match more...
1 - Реши задачи записавая решение выражением только понятно...
2 - 6. Изучи памятку. Составь словесный диафильм. Памятка.., затем...
3 - При каких значениях x трёхчлен x^2+4x−37 принимает значение,...
1 - Знайдіть довжину відрізка ED та координати його середини якщо...
3 - 1.В истории Древнего Рима существовало три периода политического...
3 - Если что ответ киньте в телегу или в ватсап здесь не чекаю +77058317795...
3 - Решите уравнение (4,5+х...
2 - Довжина прямокутника 14см ,а ширина - у 2 рази більша .знайди...
1 - Абай / жазба / негізін / қазақтың / қалады / әдебиетінің. 2....
2

3)a)
1)
Да,является
2)
3)
b)
1)
Нет, потому что прогрессия убывает.
2)
3)
c)
1)
Нет, так как прогрессия убывает
2)
3)