)3. исследуйте функцию на четность y=x^5-x^3+x. она же не четная? потому что же это кубическая парабола? правильно.? 4. найдите наим значение функции y=1+5*корень и под корнем x^2+9*. в этом я запуталась ==" тут я даже примерно написать не
могу, так что решить полностью. заранее огромное
Другие вопросы по теме Алгебра
Популярные вопросы
- Антарктида да неге суық жер...
1 - 21 a ³ b ²C определить коэффициент и степень одночлена...
3 - Complete with a verb in the present simple...
1 - n(Ca3(PO4)2)=8моль m-? m(Al(NO3)3)=18г n-?...
2 - Задание 1 Прочитайте текст, выполните задания [ ]О погоде Если в течение...
1 - Сравни дроби 14/7и 5 /21 3/10 и 8/15 13/16и 15/32 11/1и13/16...
2 - (х^4)^5×х^2/х^12 выполни действия ...
1 - Дайте розгорнуту відповідь на питання. 1. Чим безумовні рефлекси відрізняються...
3 - Опиши жизненный цикл растения опиши имено опиши...
2 - В библиотеке имеется 75000 книг, среди которых 25% детские книги, а...
2
это не кубическая парабола.
------------------------------------------------------
Дано функция f(x) = x;
Если функция четная, то f(-x) = x.
Если не четная, то f(-x) = -x.
------------------------------------------------------
Рассмотрим эту ф-цию:
f(x) = y=x^5-x^3+x;
Найдем значение в точке -х:
f(-x) = (-x)^5 -(-x)^3 + (-x)
Так, как в нас степень нечетная, то:
f(-x) = (-x)^5 -(-x)^3 + (-x) = -x^5 + x^3 - x;
вынесем минус:
f(-x) = -(x^5 - x^3 + x);
Итак, мы имеем, что : f(-x) = -x, значит ф-ия f(x) - нечетная.
------------------------------------------------------------------------------------------------
Найдем найменшее значений ф-кции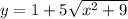
Так, как в нас есть квадратный корень(а он всегда больше или равен нулю), то
найменшее значение y будет тогда, когда мы найдем найменшее значение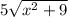 :
: 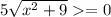
Поднесем к квадрату:
у = 1 + 5*3 = 1 + 15 = 16.