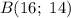269.
Какая из точек A (12; 13) или
B (16; 14) ближе к окружности
x² + y² - 8x - 46y + 343 = 0?
Другие вопросы по теме Алгебра
Популярные вопросы
- Биография и описание глечика из повести журавлиный крик...
2 - На угле ничего не растёт, на железе тоже. даже на куске золота,...
2 - Рассчитайте эквивалентное количество серной кислоты, необходимой...
3 - Укажите 2 сходства в общественном устройстве саков и усуней...
2 - Дано: треугольник abc, ad - биссектриса, d лежит на bc, be пересекает...
2 - Решите уравнение x квадрате минус 6 делёное на x - 3 равно икс деленное...
1 - Укажите предложение, средством выразительности в котором является...
3 - Краткий пересказ наталка полтавка...
3 - 5класс. решите 20 из двух одинаковых кубиков сложили параллелепипед....
1 - Жұлынның қызметі туралы мəлімет паж...
3
Составим из этого уравнения стандартное уравнение окружности:
Имеем уравнение окружности с центром в точке и радиусом
и радиусом 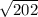
Точка будет ближе к окружности та, которая при подстановке ее координат в уравнение окружности, будет ближе к значению ее радиуса в квадрате.
Точка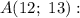
Точка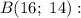
Таким образом,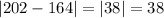 и
и 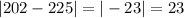
Точка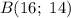 находится ближе к окружности.
находится ближе к окружности.
ответ: