25б
при каких значениях v трёхчлен −v2−13v−136 принимает неположительные значения?

выбери правильный вариант ответа:
другой ответ
v∈r
v∈(−∞; −16)
v∈[−16; +∞)
v∈(−∞; −16)∪(−16; +∞)
v∈(−∞; −16]∪[0; +∞)
v∈(−16; +∞)
v∈(−∞; −16)∪(0; +∞)
∅

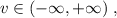ответ:     или   .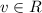

Объяснение:

P.S.  Так как D<0 , то корней нет, то есть нет точек пересечения графика параболы с осью ОV (OX). А вся парабола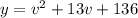     лежит выше оси ОV (аналог оси ОХ), т.к. a=+1>0. Значит для всех действительных значений переменной "v" значения функции больше нуля: у>0.

−v²−13v−136 ≤0; -(v²+13v+136) ≤0; v²+13v+136≥0;

D=169-4*136<0; а>0; поэтому v²+13v+136>0; при  любом значении v

ответ v∈(-∞;+∞)