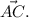2. выражение: ac+bb1+ba+d1b+b1d1+dc, если abcda₁b₁c₁d₁ - параллелепипед. а) ac; б)0 ; в)bb1; г)dc ; д)ba .
Другие вопросы по теме Алгебра
Популярные вопросы
- подготовить сообщение на форуме для подростков, описывающее событие с заголовком...
2 - Фонетический разбор слово (в казахском) : мугалем , окулык 5 класс даю...
1 - 1 Уравнения движения мотоциклиста и велосипедиста описываются закономерностями:...
2 - Здравствуйте! Хочу проверить домашнее задание сделать упражнение 43....
3 - с англиском задание 6 класса...
1 - Помагит ♡♡♡) 5 Answer the questions. 1 What is the Fab Tab ideal for? 2 Where...
2 - Собери буквы и впиши полученное слово в квадратики. Пеирнодероивед...
1 - Твір актуальність в суспільстві...
1 - Божествинна комедія Знайдіть в поемі слова, що написані на вході до Пекла 2....
2 - Конспекты по темам Функциональные разновидности языка и публицистический стиль...
1
В первой скобки применим правило треугольника, во второй скобки - правило многоугольника. Получим:
Исходное выражение примет вид:
ответ: а)