2. Доказать, что функция y =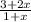 непрерывна в точке x₀=2

Question

Алгебра: 2. Доказать, что функция y = непрерывна в точке x₀=2

Nastyusha2aa5 · Answer

Функция непрерывна в какой-то точке А, если существует предел функции в точке А и он равен значению функции в точке А.

Проверим.

Значение функции у в точке х0:

$y(2) = \frac{3 + 2 \times 2}{1 + 2} = \frac{7}{3} = 2 \frac{1}{3}$

Рассчитаем предел этого выражения при х -> 2:

$lim \: \frac{3 + 2x}{1 + x} = \frac{3 + 2 \times 2}{1 + 2} = \frac{7}{3} = 2 \frac{1}{3}$

Предел и значение функции для точки х0 = 2 совпадают, значит, функция у непрерывна в точке х0 = 2.

2. Доказать, что функция y = $\frac{3+2x}{1+x}$ непрерывна в точке x₀=2